Matlab中的极坐标系和直角坐标系的相互转换
2016-12-22 21:09阅读:
极坐标系是数学中一个重要的概念,其应用领域十分广泛,包括数学、物理、工程、航海、航空以及机器人领域。
该坐标系统中任意位置可由一个夹角和一段相对原点—极点的距离来表示。
在两点间的关系用夹角和距离很容易表示时,极坐标系便显得尤为有用。
而在平面直角坐标系中,这样的关系就只能使用三角函数来表示。
对于很多类型的曲线,极坐标方程是最简单的表达形式,甚至对于某些曲线来说,只有极坐标方程能够表示。
 1.
直角坐标系
1.
直角坐标系

直角坐标系,也称笛卡儿坐标系(Cartesian
coordinatesystem
),是一种正交坐标系。
二维的直角坐标系是由两条相互垂直、0
点重合的数轴构成的。
在平面内,任何一点的坐标是根据数轴上对应的点的坐标设定的。
在平面内,任何一点与坐标的对应关系,类似于数轴上点与坐标的对应关系。
 2.
极坐标系
2.
极坐标系

极坐标系也有两个坐标轴:r(半径坐标)和
θ(角坐标、极角或方位角。r坐标表示与极点的距离,θ坐标表示按逆时针方向坐标距离0°
射线(有时也称作极轴)的角度,极轴就是在平面直角坐标系中的x
轴正方向。
比如,极坐标中的(3,
60°)
表示了一个距离极点3
个单位长度、和极轴夹角为60°
的点。(−3,
240°)
和(3,
60°)
表示了同一点,因为该点的半径为在夹角射线反向延长线上距离极点3
个单位长度的地方(240°
− 180° = 60°
)。
极坐标系中一个重要的特性是,平面直角坐标中的任意一点,可以在极坐标系中有无限种表达形式。通常来说,点(
r,
θ)
可以任意表示为(
r,
θ ±
n×360°)
或(−
r,
θ ±
(2
n +
1)180°)
,这里n是任意整数。如果某一点的r坐标为0
,那么无论θ取何值,该点的位置都落在了极点上。
 3.
极坐标系与平面直角坐标系之间的变换
3.
极坐标系与平面直角坐标系之间的变换
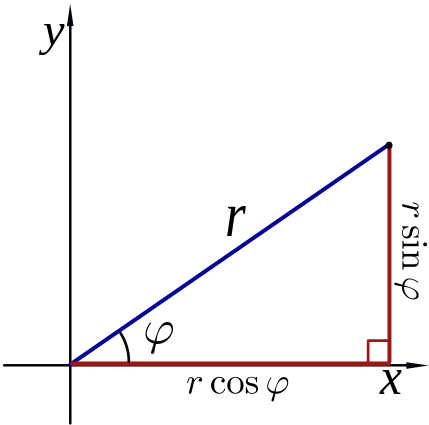
从极坐标r和θ可以变换为直角坐标:
 或
或
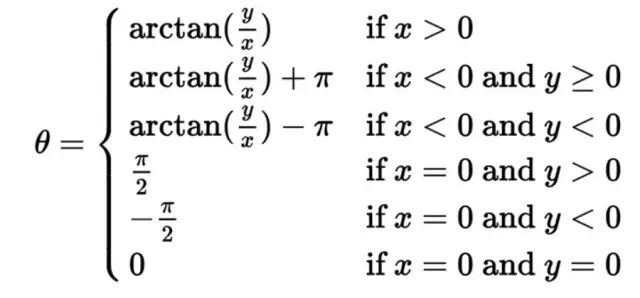
从直角坐标x
和y
也可以变换为极坐标:
 在Matlab中,仅需一行命令就可实现坐标系变换:
[theta, r]=cart2pol(x,y)
%将笛卡尔坐标转换为极坐标
[x,y]=pol2cart(theta, r)
%将极坐标转换为笛卡尔坐标
在Matlab中,仅需一行命令就可实现坐标系变换:
[theta, r]=cart2pol(x,y)
%将笛卡尔坐标转换为极坐标
[x,y]=pol2cart(theta, r)
%将极坐标转换为笛卡尔坐标
(END)

公众号:科研充电宝(原名:科学计算编点程),
不定时po一些科研干货、编程中的经验教训、实用技巧、技术宅和好玩的东西,欢迎关注~



