新浪博客

浅谈“拓扑”

2020-11-30 20:09阅读：

http://blog.sina.cn/dpool/blog/u/1175251004

字典或词典里给出“拓扑学(topology)”的意思是指对不受形状或大小变化影响的几何图形或固体物体性质的研究。在数学上，拓扑是一个非常抽象的概念，有严格的定义。本文将从简单的例子出发，力争把“拓扑”这两个字讲清楚，错误在所难免，肯请多多批评指正。本文主要分为五个部分：一、简单的例子；二、拓扑性质与拓扑变换；三、三个著名问题；四、连续、度量空间、开集和拓扑空间；五、高斯-博内定理。
一、简单的例子
先看两个简单的例子，借此说明“不受形状或大小变化影响的几何图形的性质”。例1，“平面上三角形的内角和为180度”，这是中学学到的知识，这个性质是不受三角形的形状和大小影响的。不管是普通三角形、等边三角形还是直角三角形，不管是作业本上画的小三角形还是宇宙中用三颗恒星构成的超级大三角形，内角和都是180度。强调一点，必须得是曲率为0的平面上的三角形才可以。因为正曲率曲面上的三角形内角和大于180度，负曲率曲面上的三角形内角和小于180度。平面上三角形的这个性质是一个特例，并不是严格和一般的拓扑性质，不过能够说明“不受形状或大小变化影响的几何图形的性质”。
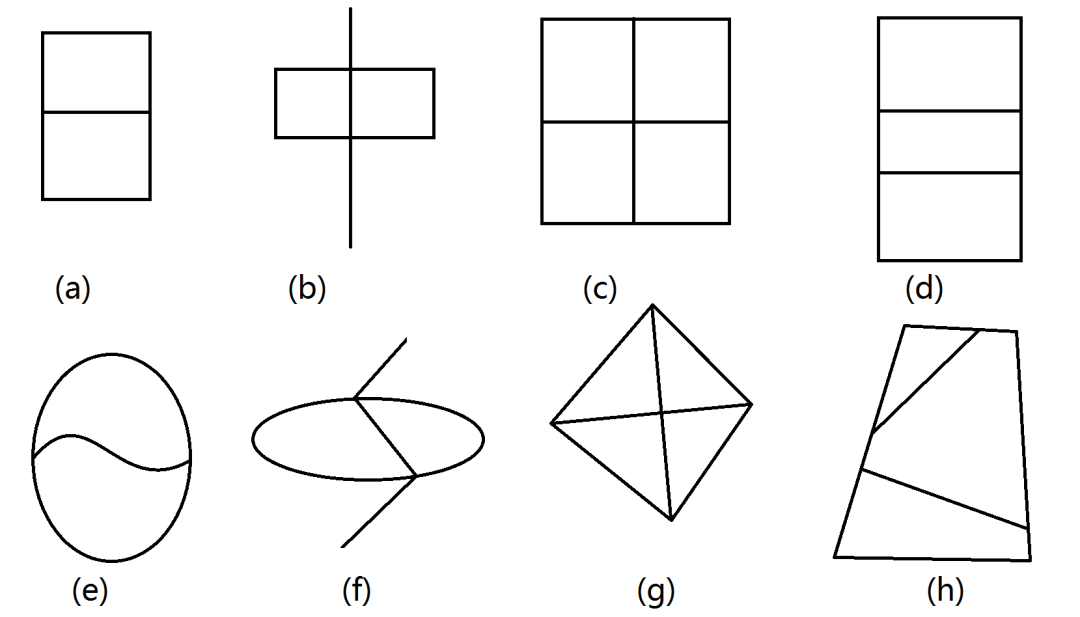
例2，见图1中的八个图形，a、b、c、d分别对应汉字中的“日”、“中”、“田”、“目”，而e、f、g、h是它们的变形。问题：“日”、“中”、“田”、“目”四个图形中哪些可以不重复地一笔画出来？哪些不能？经过尝试可以知道，“日”和“中”可以不重复地一笔画出来，而“田”和“目”则不可以。这些图形中的点可以分成两类：从一个点出发的线段的数目是奇数的称为奇点；从一个点出发的线段的数目是偶数的称为偶点。如果图形中所有的点都是偶点，就可从图形的任意点出发，不重复地把图形一笔画出。如果图形中只有两个奇点，可从其中一个奇点出发把图形不重复地一笔画出，最后回到另一个奇点。如果图形中奇点的个数多于两个，就不能把图形不重复一笔画出。
浅谈“拓扑”
图1 用于说明拓扑性质的八个平面图形（g是平面图形）
e、f、g、h分别与a、b、c、d对应，是变形后的图形，e、f与a、b一样可以一笔画出，而g、h和c、d一样不能一笔画出。“能否不重复地一笔画出来”这个性质与图形的形状和大小无关，而与线段的数目以及它们之间的连接关系有关，是拓扑性质。
二、拓扑性质与拓扑变换
图1下面图形是上面图形的变形（deformation，或者称为变换），变形之后“能否不重复地一笔画出来”这个拓扑性质（topological property）没有发生变化，那么什么样的变换才能够保证这个性质不变呢？ 在数学上这样的变换叫做“拓扑变换”，也叫“同胚(homeomorphic)映射”，定义如下：
设X和Y是拓扑空间，映射 f ：X→Y称为同胚映射，若 f 满足如下条件：1、是一一映射；2、是满射；3、是连续的映射；4、逆映射也是连续的。
在同胚映射下不变的性质称为拓扑性质。定义中拓扑空间是一个非常抽象的概念，空间两个字可以近似看成是集合（集合中含有元素），集合中定义了拓扑这个东西，就称为拓扑空间（我们将在后面对拓扑空间进行深入介绍），在拓扑空间中可以研究映射的连续性。a和e之间就存在一个同胚映射，我们以此为例进行解释。一一映射就一个点只能对应一个点，不能一个点对应多个点，也不能多个点对应一个点。满射的意思是e中不能有富余的点，就是e中的每个点都能在a中找到对应的点。连续映射其实就是要保持点的邻近性质不变，比如图a中有两个点是彼此邻近的，那么它们映射到图e中后也得是彼此邻近的才行。同胚映射，用通俗的说就是“不撕裂(tearing)，不粘连(gluing)”，但是“可弯曲，可拉伸（stretching），可压缩”。
图2给出了一个有意思的拓扑图形，问题：a和b之间存在一个同胚映射吗？简单看，似乎应该把右面的黑环断开，把白色大环拿到外面，然后再把黑环接上。这样就不是同胚映射了，因为存在撕裂和粘连。但是是存在同胚映射实现a到b的变换的，见图3，其中只利用了弯曲、拉伸和压缩，没有利用撕裂和粘连，所以图2中a和b是同胚的。
浅谈“拓扑” 图2 有意思的拓扑图形（来自网络）
浅谈“拓扑” 图3 不撕裂，不粘连的变换方法（来自网络）
三、三个著名问题
下面再举三个著名例子，这三个问题在拓扑学发展中非常重要。
1、七桥问题
见图4，有一条大河，河上有两个岛，一个大岛，一个小岛。大岛总共有4座桥与两岸相连，小岛总共有2座桥与两岸相连，两岛之间有1座桥相连。问题：一个步行者能不能不重复、不遗漏地一次走完七座桥，最后回到出发点。大数学家欧拉把它转化成一个几何图形问题，并给出了答案：不能。这个问题同样与形状和大小无关，可以抽象为b图给出的由点和线组成的图。这就是前面介绍的一笔画问题，奇点多于2个，所以不能不重复的一笔画出。
浅谈“拓扑” 图4 七桥问题（来自网络）
2、Euler定理
如果一个凸多面体的顶点数是v、棱数是e 、面数是 f ，那么它们总有这样的关系：f v – e = 2。我们可以利用图5给出的立方体做一个简单的验证，立方体的顶点数v=8、棱数e=12 、面数 f=6，可以计算出 f v – e = 2，确实符合定理。当然别的凸多面体也都符合这个定理。
浅谈“拓扑” 图5 立方体
这个的定理还存在一个等价的表达：球面上一个连通的图的节点数v (相当于凸多面体的顶点)，枝数l (相当于凸多面体的边)以及它分隔球面所成的面块数 f (相当于凸多面体的面)满足公式 f - l v = 2。见图6给出的足球，一般的标准足球是由12个正五边形和20个正六边形组成的，所以面块数 f =32。对于足球，枝数(就是两个面块的公共边界线) l = 90，节点数(就是三个面块的公共点) v = 60，通过简单的计算可知其也符合定理。
为什么是等价表达？其实很简单，把球面每个凸起面块都磨平，就是一个凸多面体。
浅谈“拓扑” 图6 足球
上面是球面上的连通图，如果换成环面（见图7）会有什么区别呢？环面上一个连通图若分隔环面成一些简单面块（即没有洞的面块），则面块数 f，图的枝数l和节点数v，满足公式 f - l v = 0。从这里可以看出球面和环面的不同，两者是拓扑不等价的，它们之间不存在拓扑变换。
浅谈“拓扑” 图7 环面（来自网络）
3、四色问题
四色问题也叫四色定理，是世界近代三大数学难题之一，难度远远大于七桥问题。这个问题说的是每幅地图都可以用四种颜色着色，使得有共同边界的国家都被着上不同的颜色。四色定理的本质是二维平面的固有属性。关于四色问题，有一个很有趣的故事，19世纪末期，有一位著名数学家闵可夫斯基，一天他刚走进教室，有一个学生就问：“如果把地图上共同边界的国家都涂成不同的颜色，那么画一幅地图只用4种颜色就够了。您能解释其中的道理吗？” 闵可夫斯基笑了笑，对学生们说：“这是一个著名的数学难题，它之所以一直没有得到解决，那仅仅是由于没有顶尖的数学家来解决它。”说完拿起粉笔，要当堂解决这个问题。下课的铃声响了，闵可夫斯基没能解决这个问题，一连好几天，他都没能解决这个问题，十分尴尬。
1976年，科学家利用电子计算机上，用了1200个小时，作了100亿个判断，最终证明了四色定理，轰动了世界。但计算机证明终究只是在庞大的数量优势上取得成功，无法给出令人信服的思考过程。这并不符合数学严密的逻辑体系，至今仍有无数数学爱好者投身其中研究。
四、连续、度量空间、开集和拓扑空间
在拓扑变换中存在一个重要的概念——“连续”(continuous)，利用“连续”才能定义拓扑变换。数学上连续映射的定义如下：设(X, d )和(Y, ρ )是两个度量空间，f 为这两个空间之间的一个映射，f : X → Y，x0 ∈ X，如果对任意 ε > 0，存在δ > 0，使得 X 中所有满足 d (x, x0 ) < δ 的 x，有
ρ ( f (x), f (x0) ) < ε
则称映射 f 在 x0 连续，若 f 在 X 的每一点都连续，则称映射 f 在 X 上连续。
前面已经介绍过连续映射是要保持点的邻近性质不变，定义中x和x0是X中邻近的两个点，映射到Y中后，变为 f(x)和 f (x0)，也是彼此邻近的，邻近是用距离这个概念表达的。定义中提到了度量空间(Metric Space)，度量就是距离，简单的说度量空间就是在元素之间定义了距离这种结构的集合，连续映射的定义中 ρ 和 d都是距离。下面给出的是度量空间的定义：
所谓度量空间（X, d），是指在其中定义了距离（或度量）d 这种结构的集合X，d 是定义在X×X上且对所有x, y, z∈X，满足以下公理的函数：
1、d(x,y) ≥0, 且d为有限的非负实数；
2、当且仅当x=y时，d(x,y)=0，；
3、d(x,y)= d(y,x)，这一条叫做对称性；
4、d(x,y) ≤ d(x, z) d(y, z) ，这一条叫做三角不等式。
这四条要求常被称为距离公理（或度量公理）。度量空间（X, d）常常被简记为X。
在连续映射的定义中利用了距离的概念，而在拓扑空间中可以不利用距离的概念而定义连续性。为了深入对此进行说明，先看下面的定理：
度量空间 X 到 Y 的映射 f 是连续的充分必要条件是Y 的任何开子集的原像是 X 的开子集，闭子集的原像是闭子集。
从这个定理可以看出，有开集的概念就可以不利用距离而直接定义连续性了。那么什么叫开集呢？
开集(open set)：若G的每一点都是内点，就称G为开集。
那么什么是内点呢？
内点：设X是度量空间，集合G ⊂X，元素x0∈X，如果存在x0的邻域{x | d(x, x0) < δ}，则称x0为G的内点。
图8给出了内点的示意图。灰色区域是集合G，x0是内点。灰色区域边界上的点不是内点，所以如果要求G是开集，那么不能包含边界。中学讲的开区间，比如（0, 1），也是不包含边界点的。
浅谈“拓扑” 图8 内点示意图
定义内点、邻域和开集都用到了距离的概念。如何脱离距离而直接定义开集呢？还得再看开集的性质。度量空间中的开集具有下列性质： 全空间和空集是开集； 任意多个开集的并是开集； 有限个开集的交是开集。
数学上可以直接利用开集的性质来定义开集。这一点如何理解呢？大家都吃过水果，但是“水果”的定义究竟应该是什么呢？水果中包含苹果、梨、西瓜等具体的水果，把苹果、梨、西瓜等具体的水果的共同性质拿出来就是水果的定义。所以水果可以定义为：富含水分的植物的果实。理解了这一点就可以看下面的拓扑空间的定义了：
设X是一个非空集合，X 的一个子集族τ称为X的一个拓扑，如果它满足：（1）X 本身和空集都属于τ；（2）τ中任意多个成员的并集仍在τ中；（3）τ中有限多个成员的交集仍在τ中。定义中的三个条件称为拓扑公理。称集合X连同它的拓扑τ为一个拓扑空间，记作（X, τ）。称τ中的成员为这个拓扑空间的开集。
定义中“子集族”就是“子集的集合”，其实就是开集的集合，“X 本身和空集都属于τ”的意思就是“全空间和空集是开集”；“τ中任意多个成员的并集仍在τ中”的意思就是“任意多个开集的并是开集”；“τ中有限多个成员的交集仍在τ中”的意思就是“有限个开集的交是开集”。拓扑空间的核心是直接利用开集的性质直接定义了开集，而不是利用距离定义开集。在拓扑空间中就可以脱离距离的定义而直接利用开集定义映射的连续性，有了连续映射，就可以定义拓扑变换进而研究拓扑性质。
五、高斯-博内定理(Gauss-Bonnet theorem)
卡尔·弗里德里希·高斯发现了该定理的一个版本但从未发表，皮埃尔·奥西安·博内1848年发表了该定理的一个特例，所以这个定理被称为高斯-博内定理。定理是关于曲面曲率的积分和拓扑间联系的一项重要表述，内容如下：
设M是一个紧的二维黎曼流形，∂M是其边界。令K为M的高斯曲率，kg为∂M的测地曲率。则有
浅谈“拓扑” 其中dA是该曲面的面积元，ds是M边界的线元。此处χ(M)是M的欧拉示性数。这个定理对于非数学专业的同学是难于理解的，不过我们可以举三个简单的例子来说明这个定理。第一个是平面上的“圆”（见图9，一个简单的二维黎曼流形），标准的圆形(半径为r)，由于在平面上，所以高斯曲率K=0，这样高斯博内定理中第一个积分为0；第二个积分是沿着边界的积分，因为圆是对称的，测地曲率为常数，kg=1/r，边界的长度为2πr，所以这个积分应该是2π，平面χ(M)=1，符合定理。
浅谈“拓扑” 图9 平面上的圆
第二个例子是球面，假设球半径为r，由于球面没有边界，所以第二个积分是0。第一个积分中，高斯曲率也是常数，K=1/r2，而圆的表面积为4πr2，所以第一个积分值为4π，球面χ(M)=2，也符合定理。当我们对球面做拓扑变换，比如变换成椭球面，那么定理也是成立的。第三个例子是环面（见图7），这时χ(M)=0，定理左面的两个积分和肯定为0。这显示出了平面、球面和环面是拓扑不等价的，欧拉示性数不同。关于环面和球面的欧拉示性数和前面介绍的关于凸多面体的Euler定理是一致的。

我的更多文章

下载客户端阅读体验更佳

APP专享