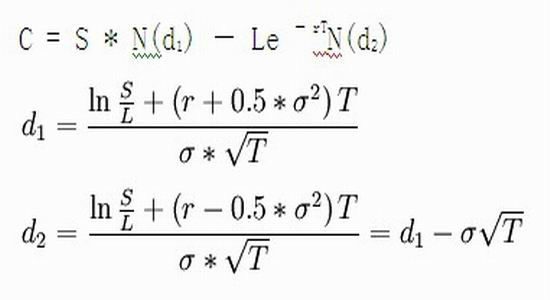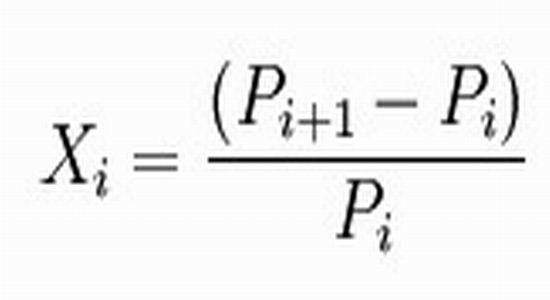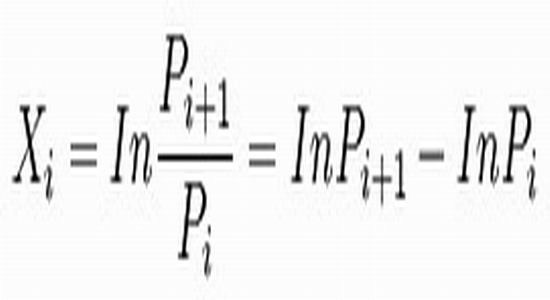果假定实际波动率是一个常数,不随时间的推移而变化,则历史波动率是实际波动率的一个很好的近似。例如,在股票市场中,历史波动率可以反映标的股票价格过去一段时期内的波动,然而,利用历史波动率对权证价格进行预测一般都不能保证准确。但是由于目前我国内地没有权证市场,无法获得权证价格,故无法计算隐含波动率,因此权证发行商与投资者在权证发行初期只能利用历史波动率作为参考。
(三)预测波动率
又称为预期波动率,一般指运用统计推断方法对实际波动率进行预测得到的结果,并可将其用于资产定价模型(例如期权定价模型),确定出资产的理论价值。因此,预测波动率是人们对权证进行理论定价时实际使用的波动率。目前,常用的计算预测波动率的方法基本上是一些统计方法,包括建立各类模型进行预测与推断,除此之外,人们对实际波动率的预测还可能来自经验判断等其他方面。
(四)已实现波动率
已实现波动率是针对频率较高的数据计算的一种波动率,又称为日内波动率或高频波动率。高频数据是指以小时、分钟或秒为采集频率的数据。还有一类数据叫超高频数据,即人们获得的股票市场、外汇市场、期货市场实时的每笔成交数据。超高频数据的时间间隔是不一定相等的,具有时变性,它是交易过程中实时采集的数据,或称逐笔数据(Tick-by-Tick
Data)。Garman & Klass(1980年)提出了日内波动率的一种估算方法—OHLC;Andersen,
Bollerslev(1998)提出使用日内高频股价数据,可以获得对日波动率更精确的描述,并由此建立了一种基于高频股价数据的已实现波动率测度方法。由于高频数据中蕴含了比低频数据更多的市场波动信息,因此基于高频数据的波动率测度一定是一种更为真实的市场波动描述。已实现波动率的计算不需要复杂的参数估计方法,无模型、计算简便,在一定条件下是积分波动率(已实现波动率的概率极限)的无偏估计量,近年来在高频领域中获得了广泛的应用。
(五)其他高频波动率
很大意义上是对已实现波动率的优化。高频数据包含了关于市场微观结构的信息,且频率越高,包含信息越多,而低频数据中,几乎不包含市场微观结构的信息。传统的经济理论通常认为市场是有效的:没有交易成本,没有摩擦,当前价格反映了所有信息、是资产的有效价格,已实现波动率即是基于资产的真实价格来估计的。但是,现实的金融市场往往并不满足有效市场的假设,存在着诸如价格离散化、非对称信息、买卖报价差(Bid-AskSpread)、不同步交易
(Asynchxonous Trading)、流动性效应 (Liquidity Effects)及闭市效应(Market
Closing)等因素,这使得观测价格偏离了资产有效价格,二者之间的差异即为市场微观结构噪声(Market
Microstructure
Noise)。抽样频率越高,由市场微观结构噪声引起的市场微观结构误差也会随着加大,从而导致日内收益率的自相关现象,使得已实现波动率不再是无偏估计量。
除市场微观结构噪声外,跳跃也会对高频数据波动的估计产生影响。早期研究中,通常假设金融资产的价格具有时间连续性,资产收益率通常进行小幅的连续平稳变化。然而,重大或异常的信息会导致资产价格产生跳跃性的变化,资产收益率在会在短时间内发生大幅波动,当有跳跃存在的时候,已实现波动也不再是无偏估计量,无法准确地对高频数据波动进行估计。随着对高频领域研究的深入,研究者们越来越重视跳跃对于资产收益率及其波动的估计和预测的影响。
此外,高频数据经常呈现出季节性,这对应用其建模的影响非常明显,因此,在进行高频数据的预测之前首先进行季节性成分的估计和数据的调整。高频数据的季节性就是通常所说的“日历效应',即金融序列的收益率和波动率呈现出日内U形。直观上理解即开盘或者收盘的时候交易都是比较活跃的,而在其他时间交易是较平淡的。为消除市场微观结构噪声、跳跃及季节性对波动率估计的影响,很多研究者提出了各种对已实现波动率进行改进的方法,包括加权已实现波动率、已实现级差波动率、加权已实现级差波动率、门限预平均已实现波动率等等。
三、波动率的计算与衡量
如前所述,波动率分为几类,不同的波动率计算与衡量的方法也不一样,大体上可以分为静态波动率估计与动态波动率估计两类,计算与估计的各类波动率均可作为实际波动率的预期值。
(一)隐含波动率的计算与衡量
是一种静态波动率的估计,假定一定时期内(期权有效期内)波动率保持不变。估计的方法有几种,包括布莱克舒尔茨公式法、Newton-Raphson迭代法、二分法等,本文主要介绍一下B-S公式法。
以无收益欧式看涨期权为例,B-S期权定价基本公式如下:
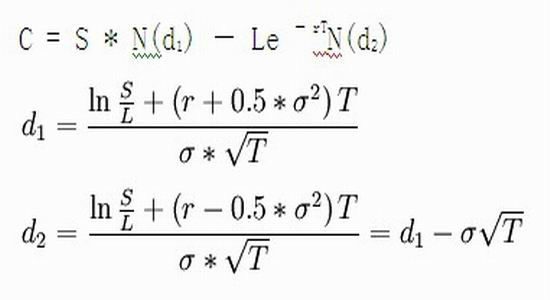
其中:
C—期权价格
L—期权执行价格
S—标的资产即期价格
T—期权有效期
r—连续复利计无风险利率
σ2—年度化方差,隐含波动率
N(d1),N(d2)—标准正态分布变量的累积概率分布函数
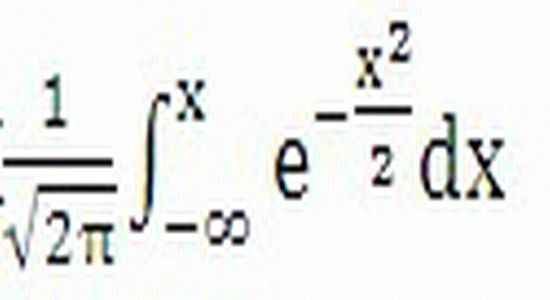
上述B-S 欧式看涨期权定价公式表明,t
时刻的期权价格是关于L、S、T、r、σ的函数,在C、L、S、T、r已知的情况下,可以由上述公式反推出市场上对标的资产从t 时刻到T
时刻波动率的估计,即隐含波动率σ2。利用市场上相同标的资产的期权反推出不同执行价格的隐含波动率,再进行插值描点就可以得到隐含波动率曲线,它反映了隐含波动率作为执行价格函数的关系。根据B-S模型的常数波动率假设,隐含波动率在一定时期内表现为一条水平线,与期权执行价格无关,也即对于同一标的资产的期权,如果期权的执行价格不同(此时期权价格也有差异),那么在同一时间点反推出的一组隐含波动率理论上应该趋同。但实证研究表明,一般情况下,同种标的资产、相同到期日的期权,协定价格由低到高偏离即期价格越多,隐含波动率往往越大,其表现在图形上似人微笑时两端上翘的嘴唇,被称为“隐含波动率的微笑”,见图1。
图1 隐含波动率随执行价格与即期价格偏差的变化
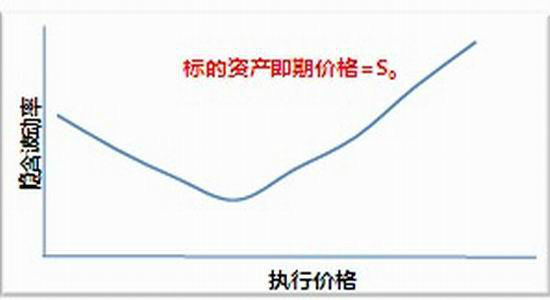
隐含波动率微笑的出现,说明根据B-S 期权定价模型得出的期权价格与实际期权价格之间出现了定价偏差,B-S
期权定价模型倾向于低估深度实值(Deep in the money)和深度虚值(Deep out of the
money)的期权价格。这体现在以期权市场价格反推隐含波动率时,深度实值和深度虚值期权的隐含波动率高于平价期权的隐含波动率。目前,对于这一现象,许多专家学者提出了一些对B-S公式及其假设进行改进的方法,该课题还在研究当中。
(二)历史波动率的计算与衡量
也是一种静态波动率的估计,假定一定时期内波动率保持不变。以股票为例:
1、从市场上获得标的股票在固定时间间隔(如每天、每周或每月等)上的价格(P1、P2、…Pi、…)。
2、对于每个时间段,求出相邻时间段股票价格变化值(收益率),这有两种方法:
(1)百分比价格变动法(即价格的环比增长速度)
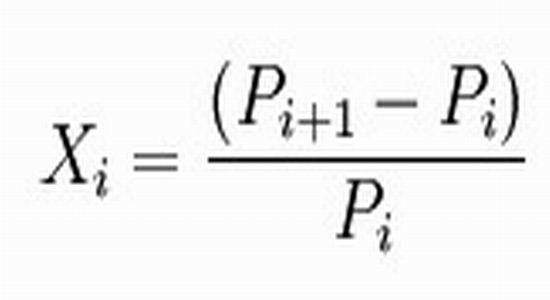
上式中,Xi是资产的百分比收益,Pi是前一时间段资产(在此指股票)的价格,Pi + 1是后一时间段资产的价格。
(2)对数价格变动法
取相邻时间段股价之比的自然对数,即
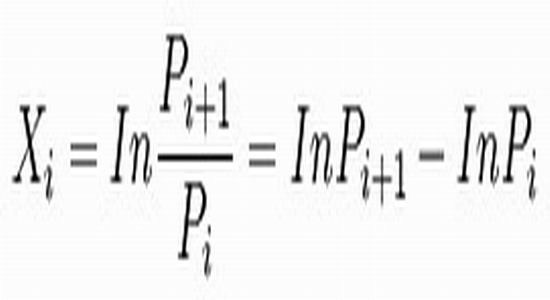
上式中,Xi是资产的对数收益,Pi是前一时间段资产的价格,Pi + 1是后一时间段资产的价格,得到序列ln(P1/
P2)、…ln(Pi/ Pi-1)…。
值得注意的是,上述两个公式的假定不一样,百分比收益公式假定有固定的不连续间隔价格变化,而对数收益公式假定价格是连续的变化。在实际中,
许多实证研究通常用对数正态分布来描述价格的分布, 特别是在金融市场的理论研究中,
如著名的B-S期权定价公式,因此,对数价格变动法经常被采用。在Black-Scholes模型中,假定价格变动是连续的,可从连续利率因子e
?rt将敲定价格换算成现值。所以,对于这个模型,对数收益公式是确定波动率的合适公式。
3、求出2中所得价格变化值的标准差σ,再乘以一定时期内(如一年)包含的时段数量的平方根(
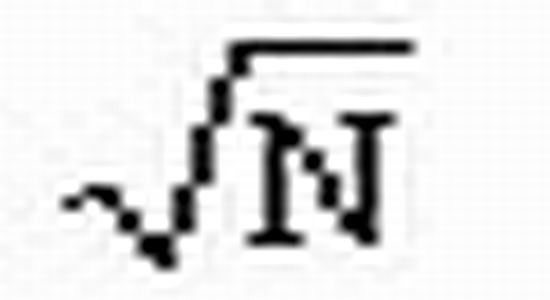
)(例如,选取时间间隔为每天,则若扣除闭市,每年中有250个交易日,应乘以
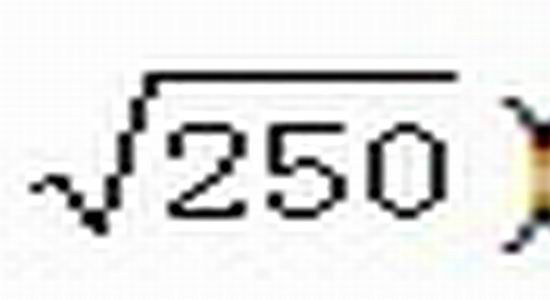
),得到的即为该时期内的历史波动率。
另有一种波动率的计算方法,在此称为HL法,即某一资产的一定时期内最高价减去最低价的值再除以最低价所得到的比率。这一方法也可以估计一定时期内的波动率的值,与历史波动率的计算方法不同,但意义相近,同样可以反映一定时期内的波动率大小,也属于一种静态估计,故在此列举出来。
(三)预测波动率的计算与衡量
多采用统计推断或动态模型来估计实际的波动率。常用的简单方法有移动平均(简单或加权)、指数平滑和条件异方差ARCH/GARCH类模型法,此外还有扩展的随机波动率模型(SV/LMSV)、多元GARCH模型法、ARIMA/ARFIMA(自回归移动平均模型)等等。以下重点介绍几种简单估计方法。
1、移动平均法

是以过去M天的收益率(一般是上述历史波动率中的对数收益率形式,也可以是其他形式的收益率)的样本方差作为当前时刻或者说当日波动率的估计值,分为简单移动平均和加权移动平均两种方法,前者将每天的收益率看成是等权重的,后者则对不同的时点赋予不同的权重。该方法需要确定的重要参数即天数M,根据经验值,对于日度数据,M一般取5或10为佳。
2、指数平滑法

借助指数平滑公式,将t时刻的波动率σ表示为t-1时刻的波动率与t-1时刻收益率r的加权平均值,式中λ为平滑系数,取值为0-1之间。将指数平滑公式通过递推推导,进一步可以得到t时刻的波动率σ与收益率r之间的关系式。该方法需要确定的重要参数即平滑系数λ,
J.P.Morgan的riskmetrics系统建议λ值随资料周期改变,并给出一个规范值,日度数据为0.94,月度数据为0.97。
3、ARCH/GARCH类模型法
是借助条件异方差动态模型的方法来估计和预测波动率。一些时间序列,特别是金融序列,常常会出现某一特征的值群集性出现的情况。例如,对股票收益率序列建模,模型的随机扰动项往往在较大幅度波动之后伴随较大幅波动,在较小幅度波动之后紧接着较小幅波动,称为波动的群集性。因此,以这类模型来估计价格或收益的波动率能更好的衡量真实波动率的变化特征。

目前,最常用的条件异方差模型是GARCH(1,1)模型,基本能反映金融时间序列方差(或波动率)的特征。
(四)已实现波动率(高频波动率/日内波动率)的计算与衡量
目前,已实现波动率一般用来表示高频数据的波动情况。常用计算方法有两种:
1、Garman & Klass(1980年)提出的日内波动率估算法—OHLC方法
此法采用样本数据日内开盘价(Open)、最高价(High)、最低价(Low)和收盘价(Close)来估计历史波动率,一般基于计算的数据频率要高于前述的一般历史波动率。取每个变量的首字母,即形成OHLC法的名称。具体公式为:
σt=【0.5×(ln(PtH/PtL ))^2-(2ln2-1)(ln(PtC / PtO ))^2】^(1/2)
σt: t时刻的波动率
PtH: t时刻的最高价
PtL: t时刻的最低价
PtO: t时刻的开盘价
PtC: t时刻的收盘价
通过实证研究发现,运用OHLC方法所计算出来的期指价格日内历史波动率具有很强的均值回归特性,它有自己运行的一个大致区间及运行规律,因此,我们对波动率规律的分析要比现指更容易一些。上述公式是从英文文献资料当中引用的,国内一些机构在使用OHLC法计算波动率时,使用的公式略有不同,调整的原因不得而知,如下:
σt=【0.5×ln(PtH/PtL )-(2ln2-1)ln(PtC / PtO )】^(1/2)
2、Andersen, Bollerslev(1998)提出的高频波动率或已实现波动率估算法
是一种非参数的方法。此法采用按照一定抽样频率的日内收益率的平方之和来估计其波动率。理论证明,在日内抽样频率选取适当的情形下,用这一方法估计出来的波动率是日收益波动率的无偏一致且有效的估计。具体公式如下:

上述公式以每五分钟的抽样频率为例,实际运用中可以根据需要选择其他的抽样频率。
四、市场波动率算法小结
目前,对波动率的相关研究很多,也衍生出许多优化的算法,各有长处。较为复杂的算法更适合理论层面的研究,一般需要借助特殊的软件实现,对于日常个人自主进行的投资研究,采用颇为简洁的计算方法更具有实用性。先将上述介绍的一些方法做一个大致的概括:
历史波动率:一定时期内各期百分比价格或价格对数收益率的标准差
HL法波动率:一定时期内最高价减去最低价的值再除以最低价所得到的比率。
隐含波动率:基础的方法是依据B-S期权定价公式推导得出
预测波动率:主要是统计推断或模型法得出
已实现波动率:OHLC法、日内或高频数据的收益率平方和作为估计值
五、波动率的应用与意义
前面介绍了几种不同的波动率,这些波动率在应用层面也发挥着不尽相同的作用。
这里将当前对波动率的主要应用层面的研究成果加以概括总结,包含以下几个方面:
(一)行情研判,指导交易
运用日内波动率,指导短线交易。OHLC方法计算出来的日内波动率具有均值回归特性,虽然来回振荡但总是向其均值方向运行,有自己运行的一个大致区间及运行规律。在每一波行情的时间段内,日内波动率都是在某一区间振荡收窄,向均值方向运行,一旦现指进入下一波阶段行情,日内波动率就会在另一个区间振荡收窄;同时,若原来波动较强烈则会突然变得相对较弱,若原来波动较弱则会出现波动突然加强,然后再进入下一波振荡区间运行。运用波动率这些规律可以指导投资者研判现货阶段行情并辅助进行趋势交易,一方面可以用来判断阶段行情的尾部,而具体后期跨入何种行情要结合基本面和其他辅助指标来进行研判。另一方面可以使得投资者在趋势交易中及时止盈离场,达到稳步盈利。例如,在一波单边上涨或者盘整行情中,若波动率宽幅振荡,一旦其波动幅度突然变小,且这种变小倾向再得到1-2个交易日的确认,则一般可以认为是此波行情的结束。即便是“伪”信号,对稳健的趋势交易者也有帮助,因为若对后期行情走势没有太大把握,可以及时平仓止盈。一般的低频数据的历史波动率也具有类似的作用,但对行情的研判侧重于大趋势方面,对频率较高的交易指导作用稍弱一些。
此外,有研究表明,在隐含波动率创出高点时也往往是市场达到底部要开始反转或反弹之时,而过低的波动率则预示着市场将会在方向上做突破,或者向上,或者向下,通常和当时市场趋势相一致。一般而言,当有类似兼并和收购的消息或者其它重大新闻发布之前,金融资产的交易(如期权)和隐含波动率会突然增长,因为获悉内幕消息者总是会提前买入或卖出,资金在短时间内流入,使期权价格偏离理论价格,推高隐含波动率,同时,交易量放大并超出平均成交量。此外,一般来说,当隐含波动率上升,代表投资者预期期货价格波动将扩大,因此权利金也会上涨;反之权利金则会下跌,投资者可以采取在隐含波动率较低时买入而在较高时卖出权证的方法来获利,至于买卖的时机可以参考隐含波动率与历史波动率进行对比的方法来确定,例如,当投资者决定了买卖方向之后,将已知或计算得到的历史波动率与隐含波动率做比较,在隐含波动率低(高)于历史波动率的时点买进(卖出)权证。
(二)指导投资资金合理配置、分散交易风险
期货交易中不同品种的价格波动幅度不同,给交易资金带来的风险度也不一样,一般而言,波动幅度越大,所带来的风险度也越大,潜在收益也越大,波动幅度越小,风险也越小,但潜在收益也越小。对于期货投资者来说,在品种间的资金配置一方面要尽量地控制好风险,同时也要尽可能地放大潜在收益,一个平衡风险与收益的方法是将交易资金分配到不同波动等级的品种上。
利用价格波动率对资金进行品种组合配置,可分步骤完成。第一步是要计算每个品种的价格波动率,参照前文列举的方法,根据需要选取一种或几种波动率进行计算;第二步是取计算得到的系列价格波动率或其平均值,作为一定时期内该品种的价格波动率数值;第三步是将得到的各品种的波动率按照数值大小划分类别,例如,按照波动率的大小可以将商品品种划分为三类:第一类是高波动性品种,第二类是中等波动性品种,第三类为低波动性品种。最后,从几类不同波动性类别中各抽出1-2个左右的品种进行搭配交易。例如,某帐户的交易资金按价格波动率大小选取了6个品种进行组合,所配置的品种为:高波动性品种黄金、中等波动性品种
大豆(3693,-28.00,-0.75%)、
燃料油(3523,-9.00,-0.25%),低波动性品种
玉米(1883,-3.00,-0.16%)、
强麦和
棉花(15350,70.00,0.46%)。通过这种波动性的组合搭配,既扩大了交易机会的选择范围,同时也达到了合理分散风险的目的。
(三)派生波动率指数及相关交易产品,预期市场波动/规避风险、丰富投资工具
Whaley(1993)提出了编制市场波动率指数作为衡量未来股票市场价格波动程度的方法,同年,芝加哥期权交易所(CBOE)开始编制VIX指数,也称为“投资者情绪指标”,以反映市场对于的未来波动程度的预期,该指数选择S&P100指数期权的隐含波动率为编制基础,同时计算买权与卖权的隐含波动率,以考虑交易者使用买权或卖权的偏好。当指数越高时,显示投资者预期未来股价指数的波动性越剧烈;当VIX指数越低时,代表投资者认为未来的股价波动将趋于缓和。在2003年推出新的VIX指数(编制基础为更有代表性的S&P500)后,旧指数仍然继续公布,更名为VXO指数。经过十多年的发展和完善,VIX指数逐渐得到市场认同,CBOE还于2001年推出了以NASDAQ100指数为标的的波动性指标
(VXN)。
CBOE于2004年推出了第一个波动率指数期货(Volatility Index
Futures)以及一个将波动性商品化的期货,方差期货(Variance
Futures),标的为三个月期的S&P500指数的现实方差。波动率交易是基于对资产/商品价格波动率的方向作出预测,其交易策略可以分为两类,做多波动率(Long
Volatility)和做空波动率(Short
Volatility),常使用的工具是期权,也可以通过期货+止损来构造类似策略。
大量研究以波动率为对象进行了实证检验,Whaley最早开始对波动性指标进行研究,并探讨其在避险方面的应用,其研究结果指出VXO指数和S&P100指数呈负相关关系;通过模拟波动性指标衍生品的避险效果,说明波动性指标可以在不影响其它风险参数的情况下,有效规避投资组合的Vega风险。
中粮期货研发部 丁睿