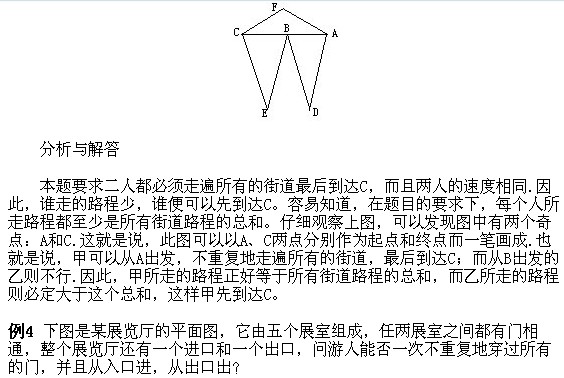
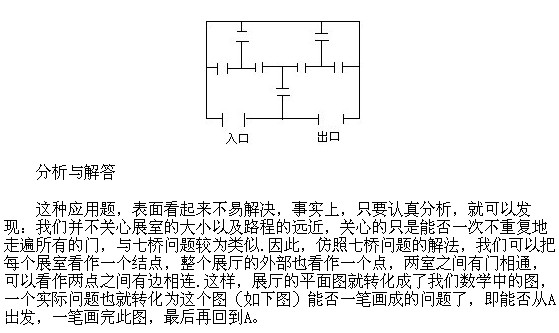
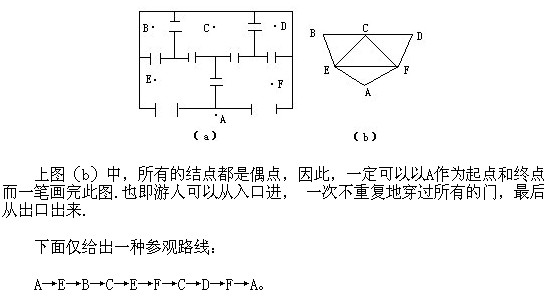
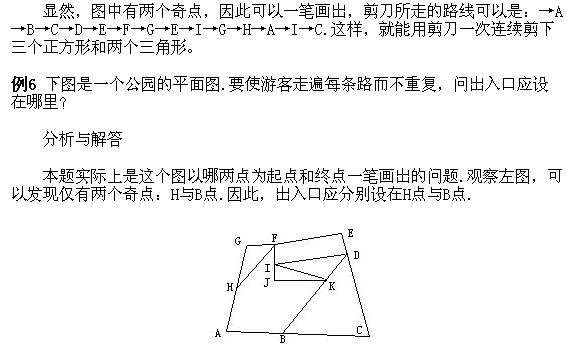
雪帆奥数开心训练讲座之一笔画问题

引子:你能一笔下来写出如下汉字吗? 田,日,中,串,白 ,百,申 。还有著名的七孔桥问题,你知道它能否一次走完所有的桥,不能重复?
问题:什么样的图形才能一笔画,如果不能一笔画,那至少几笔才能完成呢?
思考:想要了解一笔画问题,首先要了解一下一笔画的概念。很多同学在没有搞清楚概念的时候就着急做题,有的不知道怎么才算一笔画,有的不知道如何转化为一笔画,下面雪帆老师就一一详解。
一、什么是一笔画问题
雪帆答:一笔画问题,是指能否用一笔就能画出的图形问题。这里的“一笔”,是指一笔下来,不能抬起笔,而图形的每条边,都要且只能经过一次,不能重复。言外之意,图形中的点可以多次经过。
二、什么样的图形才能一笔画完成
雪帆答:只有具有以下特点的图形才能一笔画。
1、没有奇点的连通图形,能一笔画完成,出发点为任意点,并返回到原出发点。例如两个相交的圆,你可以从任意一点出发,一笔完成后回到该点。
2、只有2个奇点的连通图形,能一笔画完成,出发点为一个奇点,最终回到另外一个奇点。例如一个带有一条直径的圆,你要从直径的一端出发,一笔完成后,回到另外一个端点。
3、有2n个奇点的连通图形,至少需要n笔画完成。
三、解释理论知识中的两个概念
1、什么叫奇点和偶点
雪帆答
引子:你能一笔下来写出如下汉字吗? 田,日,中,串,白 ,百,申 。还有著名的七孔桥问题,你知道它能否一次走完所有的桥,不能重复?
问题:什么样的图形才能一笔画,如果不能一笔画,那至少几笔才能完成呢?
思考:想要了解一笔画问题,首先要了解一下一笔画的概念。很多同学在没有搞清楚概念的时候就着急做题,有的不知道怎么才算一笔画,有的不知道如何转化为一笔画,下面雪帆老师就一一详解。
一、什么是一笔画问题
雪帆答:一笔画问题,是指能否用一笔就能画出的图形问题。这里的“一笔”,是指一笔下来,不能抬起笔,而图形的每条边,都要且只能经过一次,不能重复。言外之意,图形中的点可以多次经过。
二、什么样的图形才能一笔画完成
雪帆答:只有具有以下特点的图形才能一笔画。
1、没有奇点的连通图形,能一笔画完成,出发点为任意点,并返回到原出发点。例如两个相交的圆,你可以从任意一点出发,一笔完成后回到该点。
2、只有2个奇点的连通图形,能一笔画完成,出发点为一个奇点,最终回到另外一个奇点。例如一个带有一条直径的圆,你要从直径的一端出发,一笔完成后,回到另外一个端点。
3、有2n个奇点的连通图形,至少需要n笔画完成。
三、解释理论知识中的两个概念
1、什么叫奇点和偶点
雪帆答