新浪博客
它是发散的。
 的级数:
的级数:
函数 是黎曼ζ函数在实轴大于1的部分的限制,关于黎曼ζ函数有著名的黎曼猜想。
是黎曼ζ函数在实轴大于1的部分的限制,关于黎曼ζ函数有著名的黎曼猜想。
 在一点
在一点  附近取值的级数。泰勒函数由函数在点
附近取值的级数。泰勒函数由函数在点  的各阶导数值构成,具体形式为:
的各阶导数值构成,具体形式为:
 附近收敛,那么就称函数
附近收敛,那么就称函数  在点
在点  上是解析的。
上是解析的。
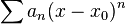 的函数项无穷级数称为
的函数项无穷级数称为  的幂级数。它的收敛与否和系数
的幂级数。它的收敛与否和系数  有关。
有关。
例如,周期为 的周期函数
的周期函数  可以表示为:
可以表示为:
 ,
,  ,特别的,
,特别的, 
p-级数
p-级数是指通项为 的级数:
的级数:函数
 是黎曼ζ函数在实轴大于1的部分的限制,关于黎曼ζ函数有著名的黎曼猜想。
是黎曼ζ函数在实轴大于1的部分的限制,关于黎曼ζ函数有著名的黎曼猜想。裂项级数
泰勒级数
泰勒级数是关于一个光滑函数 在一点
在一点  附近取值的级数。泰勒函数由函数在点
附近取值的级数。泰勒函数由函数在点  的各阶导数值构成,具体形式为:
的各阶导数值构成,具体形式为: 附近收敛,那么就称函数
附近收敛,那么就称函数  在点
在点  上是解析的。
上是解析的。交错级数
具有以下形式的级数幂级数
形同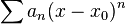 的函数项无穷级数称为
的函数项无穷级数称为  的幂级数。它的收敛与否和系数
的幂级数。它的收敛与否和系数  有关。
有关。傅里叶级数
任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示,称为傅里叶级数。傅里叶级数是函数项无穷级数,也就是说每项都是一个函数。傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用。例如,周期为
 的周期函数
的周期函数  可以表示为:
可以表示为: ,
,  ,特别的,
,特别的, 


 收敛当且仅当 |z| < 1。
收敛当且仅当 |z| < 1。 的级数:
的级数: