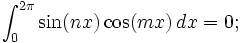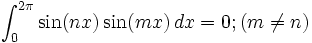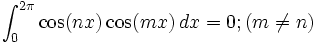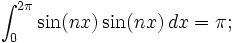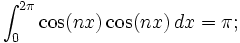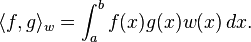各种正交概念

2009-10-21 21:12阅读：

http://blog.sina.cn/dpool/blog/u/1310590113

函数的正交是向量正交的推广,函数可看成无穷维向量,在n维空间中两向量正交是借助内积来定义的,设X=(x1,x2,...,xn),Y=(y1,y2,...,yn),则X与Y正交定义为其内积XY=x1y1+x2y2+...+xnyn=0,
设f(x),g(x)是定义在[a,b]区间的可积函数,f(x),g(x)中的自变元类似于(有限维)向量下标,向量X中分量的下标取1,2,..,n这些离散值,而f(x)中的x可连续取[a,b]中所有的值,因此f(x)是无穷维向量,两向量内积是对应分量之积的有限和,推广到函数空间,两函数内积是对应分量(函数值)之积的无限和,积分是有限和的极限,因此积分表示一个无限和,为了看清这一推广,将向量内积表示为XY=x1y11+x2y21+...+xnyn*1,这个和式中每一项是由X的分量,Y的分量和1相乘之积(1看成下标取1个单位),对应于向量内积的写法,函数内积应写为f(x)g(x)△x,它对应了[a,b]区间某子区间的值,该子区间长为△x,它类似于下标,将所有这些值加起来,当最大子区间长为趋于零,有限和变为无限和,其值恰为f(x)g(x)在[a,b]的积分.

三角函数族的正交性

所谓的两个不同向量正交是指它们的内积为0，这也就意味着这两个向量之间没有任何相关性,例如，在三维欧氏空间中，互相垂直的向量之间是正交的。事实上，正交是垂直在数学上的的一种抽象化和一般化。一组n个互相正交的向量必然是线性无关

的，所以必然可以张成一个n维空间，也就是说，空间中的任何一个向量可以用它们来线性表出。三角函数族的正交性用公式表示出来就是：

$\int _{0}^{2\pi}\sin (nx)\cos (mx) \,dx=0;$

$\int _{0}^{2\pi}\sin (nx)\sin (mx) \,dx=0;(me n)$

$\int _{0}^{2\pi}\cos (nx)\cos (mx) \,dx=0;(me n)$

$\int _{0}^{2\pi}\sin (nx)\sin (nx) \,dx=\pi;$

$\int _{0}^{2\pi}\cos (nx)\cos (nx) \,dx=\pi;$

正交函数集

对于两个函数 f 和g，可以定义如下的内积:

$\langle f, g\rangle_w = \int_a^b f(x)g(x)w(x)\,dx.$

这里引进一个非负的权函数w(x)。这个内积叫做带权w(x)的内积。
两个函数带权w(x)正交，是指它们带权w(x)的内积为零。

$\int_a^b f(x)g(x)w(x)\,dx = 0.$

由此可以类似定义带权w(x)的模型。

$||f||_w = \sqrt{\langle f, f\rangle_w}$

一个函数列{ f_i : i = 1, 2, 3, ... }如果满足：

$\langle f_i, f_j \rangle=\int_{-\infty}^\infty f_i(x) f_j(x) w(x)\,dx=||f_i||^2\delta_{i,j}=||f_j||^2\delta_{i,j}$

就称为带权w(x)的正交函数族。
如果满足：

$\langle f_i, f_j \rangle=\int_{-\infty}^\infty f_i(x) f_j(x) w(x)\,dx=\delta_{i,j}$

其中

$\delta_{i,j}=\left\{\begin{matrix}1 & \mathrm{if}\ i=j \\ 0 & \mathrm{if}\ ieq j\end{matrix}\right\}$

为克罗内克函数。

就称为带权w(x)的标准正交函数族

正交子空间

若内积空间中两向量的内积为0，则它们正交。类似地，若内积空间中的向量v与子空间A中的每个向量都正交，那么这个向量和子空间A正交。若内积空间的子空间A和B满足一者中的每个向量都与另一者正交，那么它们互为正交子空间。

正交变换

正交变换 $T <wbr>: V \rightarrow V$ 是保持内积的线性变换。即是说，对两个向量，它们的内积等于它们在函数T下的内积：

$\langle Tx, Ty \rangle = \langle x, y \rangle.$

这也就是说，正交变换保持向量的长度不变，也保持两个向量之间的角度不变。

欧几里得空间的例子

在二维或三维的欧几里得空间中，两个向量正交当且仅当他们的点积为零，即它们成90°角。可以看出正交的概念正是在此基础上推广而来的。三维空间中，一条直线的正交子空间是一个平面，反之亦然。四维空间中，一条直线的正交子空间则是一个超平面。

举报/Report

我的更多文章

下载客户端阅读体验更佳