凸包与凸多边形的定义
2018-12-25 10:02阅读:
转自https://wiki.mbalib.com/wiki/凸包
凸包(Convex hull)
什么是凸包
在了解凸包之前,须先
认识何谓“凸多边形”(Convex
Polygon)。从直观上说,一个凸多边形就是没有任何凹陷位的多边形。我们在低年级数学所学习的三角形、正方形、长方形、平行四边形、正五边形、正六边形等等,都是凸多边形的例子。但是以下这个“凸”字形却并非凸多边形,因为箭头指着的地方实际是一个凹陷位。
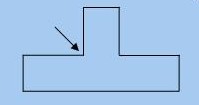

可是上述这一定义很不严密,究竟何谓“凹陷位”?实在难以说清楚。因此在数学上,凸多边形有另一个严格的
定义。假设我们在一个多边形上(包括多边形的边界及边界围封的范围)任意取两点并以一条线段连结该两点,如果线段上的每一点均在该多边形上,那么我们便说这个多边形是凸的。根据以上定义,我们便可判断“凸”字形的确不是凸的。例如,在下图中,连结A、B两点的线段有一部分并不在该多边形上。


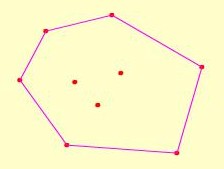
认识了凸多边形后,我们便可了解何谓凸包。给定平面上的一个(有限)点集(即一组点),这个点集的凸包就是包含点集中所有点的最小面积的凸多边形。例如,下图的点集共包含9个点,图中的六边形便是该点集的凸包。其中构成六边形的6个点称为“凸包上的点”(Hull
Point),其余3个点则并非“凸包上的点”。请注意上述定义中“最小面积”这个限制条件,因为除了凸包以外,还有无限多个包含点集中所有点的凸多边形。例如,只要画一个面积足够大的四边形,便可包围任意给定的点集。因此假如没有这个限制条件,求凸包就变成非常容易但却没有唯一解的运算。

转自
https://baike.baidu.com/item/凸多边形/6608474?fr=aladdin
凸多边形是一个内部为凸集的简单多边形。凸多边形(Convex
Polygon)指如果把一个多边形的所有边中,任意一条边向两方无限延长成为一直线时,其他各边都在此直线的同旁,那么这个多边形就叫做凸多边形,其内角应该全不是优角,任意两个顶点间的线段位于多边形的内部或边上。
凸多边形(Convex Polygon)可以有以下三种定义:
- 没有任何一个内角是优角(Reflexive Angle)的多边形。
- 如果把一个多边形的所有边中,有一条边向两方无限延长成为一直线时,其他各边都在此直线的同旁,那么这个多边形就叫做凸多边形。
[1]
- 凸多边形是一个内部为凸集的简单多边形。简单多边形的下列性质与其凸性等价:1、所有内角小于等于180度。2、任意两个顶点间的线段位于多边形的内部或边上。3、多边形内任意两个点,其连线全部在多边形内部或边上。
凸包法求正方形个数
16个钉子摆成4x4方阵,以其中4个为顶点用皮筋围成正方形,可以围成多少个?
【3*3*1+2*2*2+1*1*3】





