新浪博客
是位置, 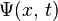 是相依于时间
是相依于时间  的波函数,
的波函数,
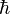 是约化普朗克常数,
是约化普朗克常数,
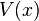 是位势。
是位势。
类似地,在三维空间里,一个单独粒子运动于位势 中的含时薛定谔方程为
中的含时薛定谔方程为
 个粒子,则波函数是定义于
个粒子,则波函数是定义于  -位形空间,所有可能的粒子位置空间。用方程表达,
-位形空间,所有可能的粒子位置空间。用方程表达,
 的第
的第 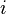 个参数是第
个参数是第 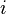 个粒子的位置。所以,第
个粒子的位置。所以,第 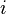 个粒子的位置是
个粒子的位置是  。
。
不含时薛定谔方程
不含时薛定谔方程不相依于时间,又称为本征能量薛定谔方程,或定态薛定谔方程。顾名思义,本征能量薛定谔方程,可以用来计算粒子的本征能量与其它相关的量子性质。
应用分离变量法,猜想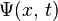 的函数形式为
的函数形式为
 是分离常数,
是分离常数,  是对应于
是对应于  的函数.稍回儿,我们会察觉
的函数.稍回儿,我们会察觉  就是能量.
就是能量.
代入这猜想解,经过一番运算,含时薛定谔方程 (1) 会变为不含时薛定谔方程:
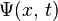 是相依于时间
是相依于时间  的波函数,
的波函数,
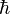 是约化普朗克常数,
是约化普朗克常数,
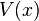 是位势。
是位势。类似地,在三维空间里,一个单独粒子运动于位势
 中的含时薛定谔方程为
中的含时薛定谔方程为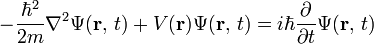 。(2)
。(2)
 个粒子,则波函数是定义于
个粒子,则波函数是定义于  -位形空间,所有可能的粒子位置空间。用方程表达,
-位形空间,所有可能的粒子位置空间。用方程表达,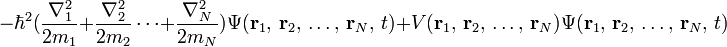
 。
。
 的第
的第 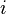 个参数是第
个参数是第 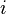 个粒子的位置。所以,第
个粒子的位置。所以,第 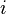 个粒子的位置是
个粒子的位置是  。
。不含时薛定谔方程
不含时薛定谔方程不相依于时间,又称为本征能量薛定谔方程,或定态薛定谔方程。顾名思义,本征能量薛定谔方程,可以用来计算粒子的本征能量与其它相关的量子性质。
应用分离变量法,猜想
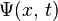 的函数形式为
的函数形式为 ;
;
 是分离常数,
是分离常数,  是对应于
是对应于  的函数.稍回儿,我们会察觉
的函数.稍回儿,我们会察觉  就是能量.
就是能量.代入这猜想解,经过一番运算,含时薛定谔方程 (1) 会变为不含时薛定谔方程:
 。
。

- 含时薛定谔方程导引
启发式导引
含时薛定谔方程的启发式导引,建立于几个假设:
假设
(1) 一个粒子的总能量 可以经典地表达为动能
可以经典地表达为动能  与势能
与势能  的和:
的和:
 ;
;
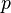 是动量,
是动量, 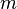 是质量。
是质量。
特别注意,能量 与动量
与动量 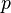 也出现于以下两个关系方程。
也出现于以下两个关系方程。
(2) 1905年,爱因斯坦于提出光电效应时,指出光子的能量 与对应的电磁波的频率
与对应的电磁波的频率
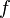 成正比:
成正比:
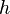 是普朗克常数,
是普朗克常数,
 是角频率。
是角频率。
(3) 1924年,路易·德布罗意提出德布罗意假说,说明所有的粒子都具有波的性质,可以用一个波函数 来表达。粒子的动量
来表达。粒子的动量 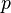 与伴随的波函数的波长
与伴随的波函数的波长  有关:
有关:
 ;
;
 是波数。
是波数。
用矢量表达, 。
。
波函数以复值平面波来表达波函数
1925年,薛定谔发现平面波的相位,可用一个相位因子来表示:
 。
。
 ,
,

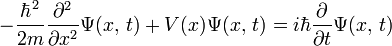 ;
;