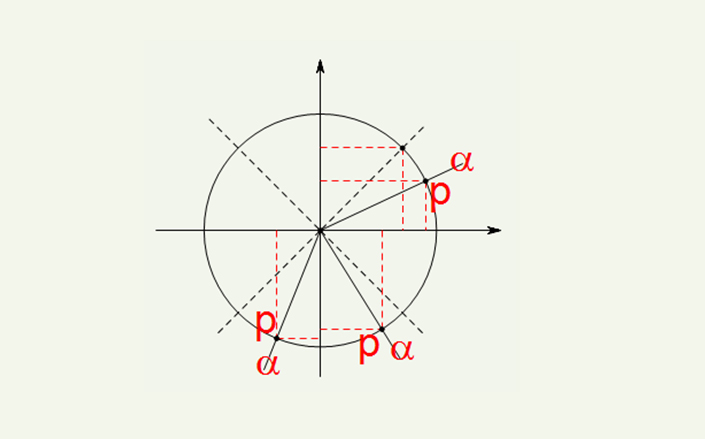
先讲一下角的正弦、余弦在单位圆中的表示,如图,黑色虚线是象限的角平分线,角α的终边与单位圆交于点P,则点P的横坐标就是角α的余弦,纵坐标就是角α的正弦;当角α的终边OP绕着坐标原点旋转时,点P的横纵坐标(角α的余弦、正弦)在不断的变化,咱们需要掌握的就是,在这个旋转的过程中,点P的横纵坐标(角α的余弦、正弦)的符号以及大小是如何变化的。
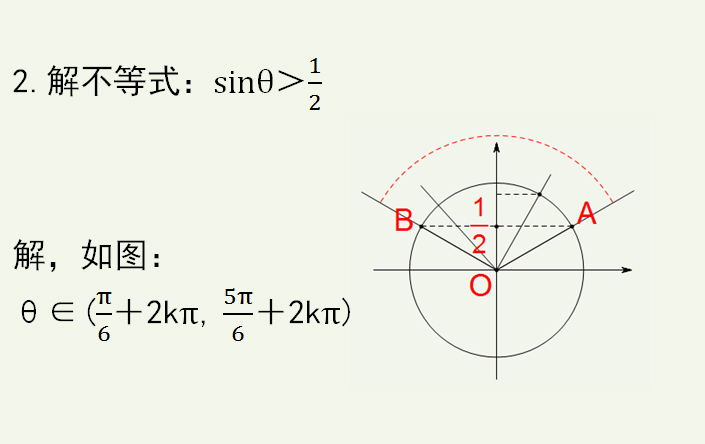
例如,OP以x轴正半轴为起点绕着原点逆时针方向旋转,角α的余弦(点P横坐标)为正数,且从1不断减小,角α的正弦(点P纵坐标)为正数,且从0不断增大,此时余弦大于正弦,当OP与第一象限角平分线重合时,角α的余弦、正弦正好相等,之后余弦小于正弦;再如,当OP旋转到与y轴负半轴重合开始,进入第四象限,余弦值为正数,且越来越大,正弦值为负数,也越来越大,当OP与第四象限角平分线重合时,角α的余弦、正弦的绝对值正好相等。大家可以用这种方法自己分析各个象限的情况,多练几次,就熟练了。学会熟练使用单位圆,能使你在解决三角函数部分的各种计算中得心应手。

第1题分析:本题考查使用单位圆判断正弦、余弦的符号;本题是3个三角函数相乘,分别判断每一项的符号即可;分析第1项cos(sinθ):把sinθ的值看做角的大小,sinθ∈[-1,1],[-1,1]包含于(-π/2, π/2),根据上面的单位圆很容分析出其余弦值cos(sin

例如,OP以x轴正半轴为起点绕着原点逆时针方向旋转,角α的余弦(点P横坐标)为正数,且从1不断减小,角α的正弦(点P纵坐标)为正数,且从0不断增大,此时余弦大于正弦,当OP与第一象限角平分线重合时,角α的余弦、正弦正好相等,之后余弦小于正弦;再如,当OP旋转到与y轴负半轴重合开始,进入第四象限,余弦值为正数,且越来越大,正弦值为负数,也越来越大,当OP与第四象限角平分线重合时,角α的余弦、正弦的绝对值正好相等。大家可以用这种方法自己分析各个象限的情况,多练几次,就熟练了。学会熟练使用单位圆,能使你在解决三角函数部分的各种计算中得心应手。

第1题分析:本题考查使用单位圆判断正弦、余弦的符号;本题是3个三角函数相乘,分别判断每一项的符号即可;分析第1项cos(sinθ):把sinθ的值看做角的大小,sinθ∈[-1,1],[-1,1]包含于(-π/2, π/2),根据上面的单位圆很容分析出其余弦值cos(sin