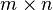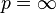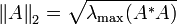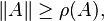矩阵范数(martix norm) --维基百科
2011-11-12 15:58阅读:
矩阵范数(martix
norm)是数学上向量范数对矩阵的一个自然推广。
[编辑]矩阵范数的特性
以下
K
代表
实数或
复数域。现在考虑

空间,亦即所有
m 行与
n
列的矩阵。

上的矩阵范数满足向量范数的所有特性,即若

是矩阵
A 的范数,那么:
 ,且等号成立当且仅当
A = 0
。
,且等号成立当且仅当
A = 0
。
 ,对于所有
α 属于
K
和所有矩阵 A 属于
,对于所有
α 属于
K
和所有矩阵 A 属于
 成立。
成立。
 ,对于所有矩阵
A
和 B 属于
,对于所有矩阵
A
和 B 属于

此外,一些定义在
n乘
n矩阵上的矩阵范数(但并非所有这类的范数)满足一个或多个以下与“矩阵比纯粹一个向量有更多东西的事实”有关的条件:
一个满足第一个附加特性的矩阵范数被称为
服从乘法范数(
sub-multiplicative norm)。附上矩阵范数并包含所有
n×
n
矩阵的集合,是
巴拿赫代数的一个例子。
(在一些书上,术语“矩阵范数”只指服从乘法范数。)
[编辑]诱导范数
如果
Km
及
Kn
上
向量范数已知(
K
是
实数或
复数域),可在
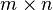
矩阵空间上按照下述原则定义相应的“诱导范数”或
算子范数:

若
m =
n
且在定义域和值域上使用相同的范数,则诱导的算子范数是服从乘矩阵范数。
举例说明, 与向量的
p-范数对应的算子范数是:

在
p = 1
且
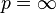
的情况下,其范数可以以下方式计算:

这些与矩阵的 Schatten
p-范数不同, 也可以用

来表示。
若满足
p = 2(
欧几里德范数)且
m =
n(方阵)此两特殊情况时,诱导的矩阵范数就是“谱范数”。矩阵
A 的谱范数是
A 最大的
奇异值或
半正定矩阵
A*A
的最大
特征值的平方根:
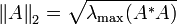
其中
A* 代表
A 的
共轭转置
。
任何矩阵范数满足此不等式
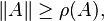
其中 ρ(
A



 ,且等号成立当且仅当
,且等号成立当且仅当
 ,对于所有
,对于所有

 ,对于所有矩阵
,对于所有矩阵

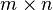
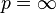




 ,且等号成立当且仅当
,且等号成立当且仅当
 ,对于所有
,对于所有

 ,对于所有矩阵
,对于所有矩阵