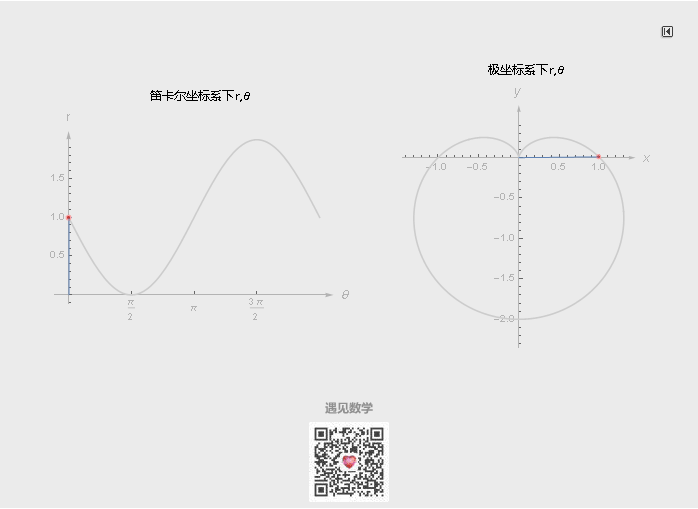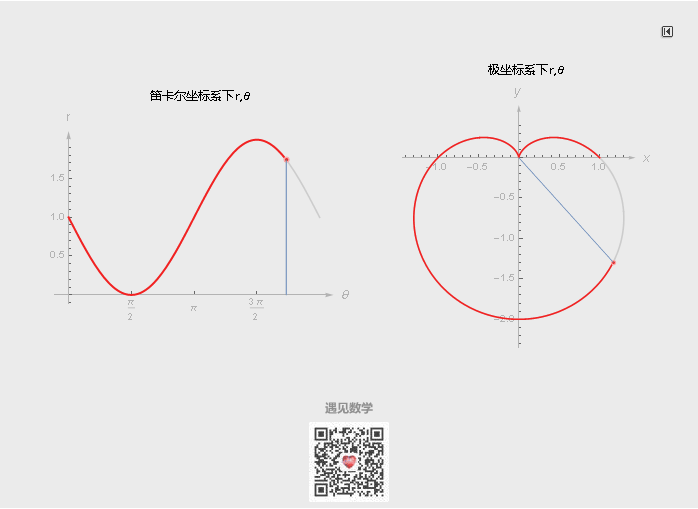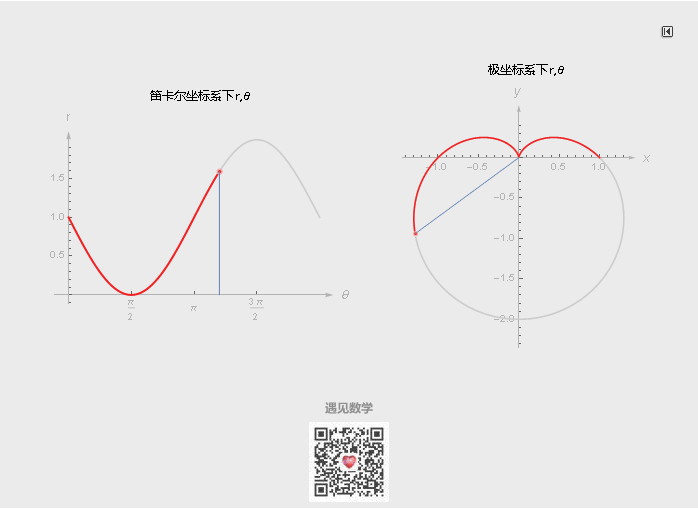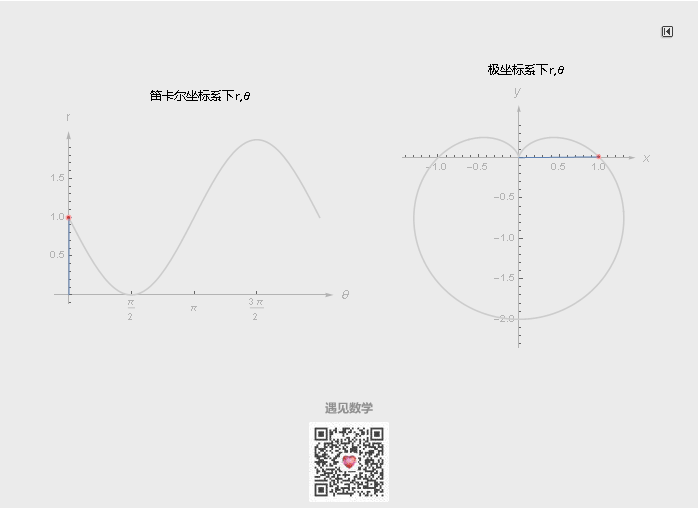
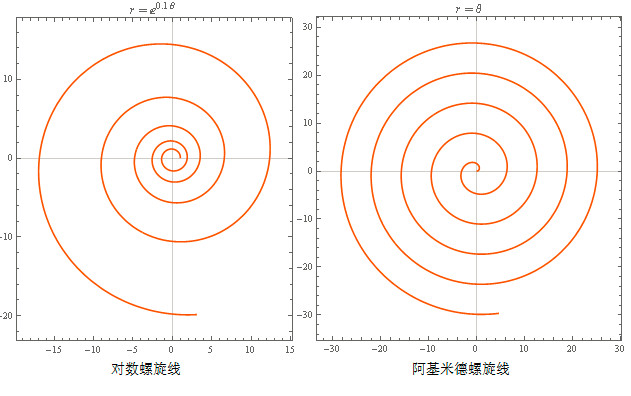
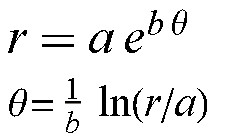坐标系只是人们描述空间任意位置的一种方法, 除了笛卡尔坐标系, 最常见到的还有极坐标系, 有时候用极坐标来表示函数会更简洁, 甚至对某些曲线而言, 只有极坐标能够表示.
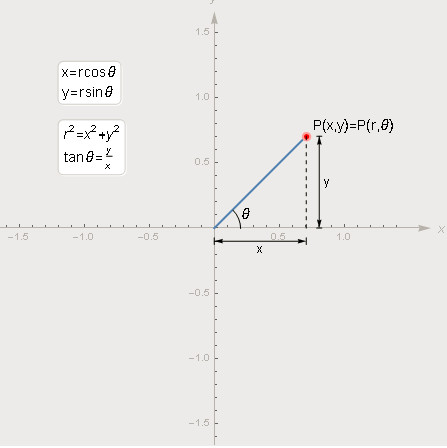
有了 r 和
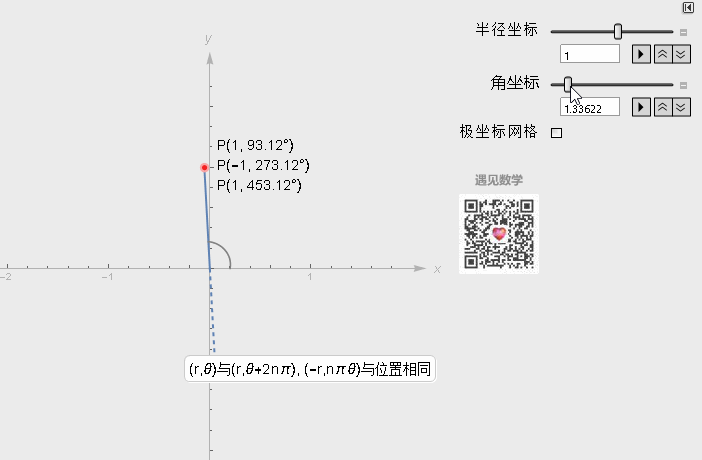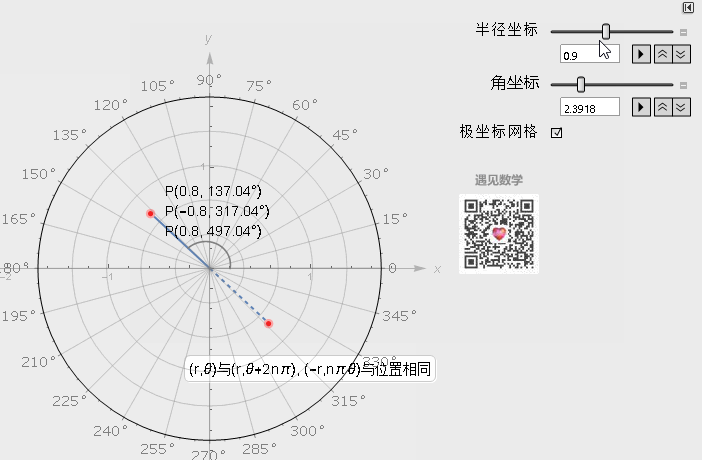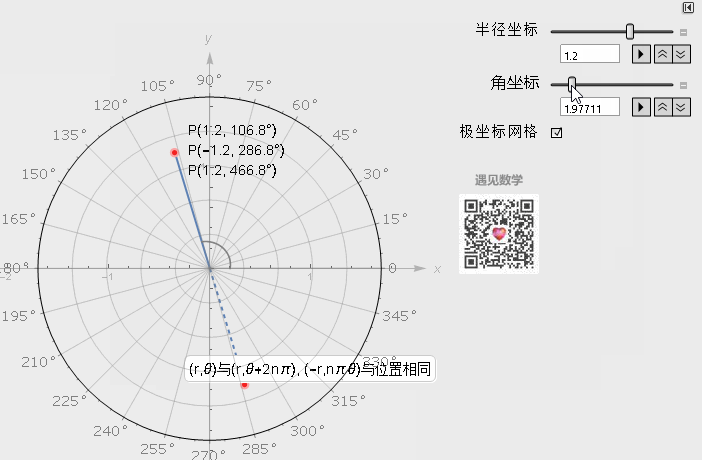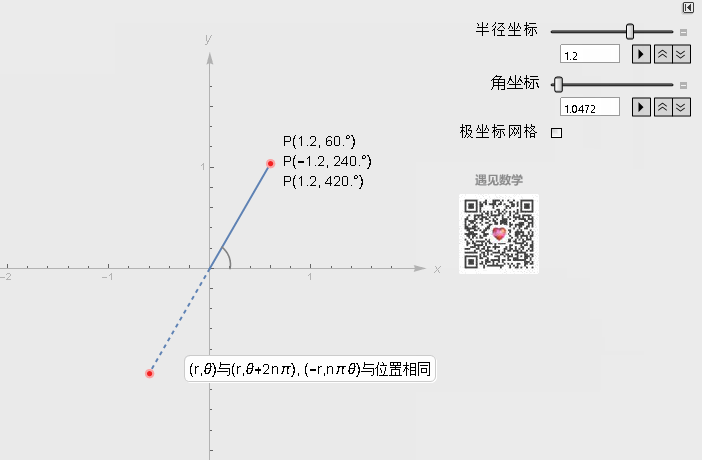
极坐标系中一个重要的特性是, 平面直角坐标中的任意一点, 可以在极坐标系中有无限种表达形式. 通常来说, 点(r, θ)可以任意表示为(r, θ ±
坐标系只是人们描述空间任意位置的一种方法, 除了笛卡尔坐标系, 最常见到的还有极坐标系, 有时候用极坐标来表示函数会更简洁, 甚至对某些曲线而言, 只有极坐标能够表示.
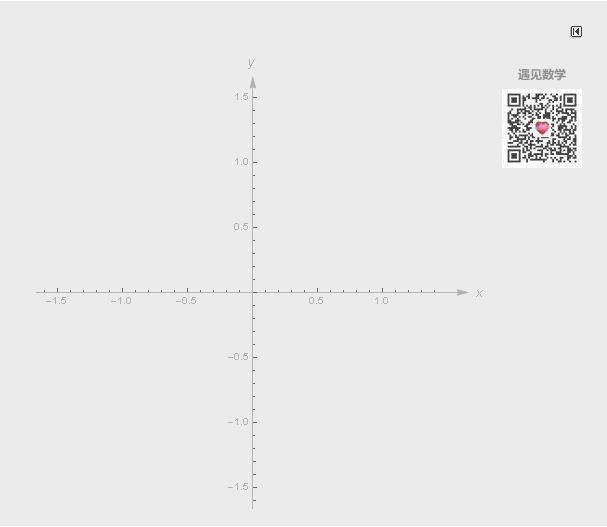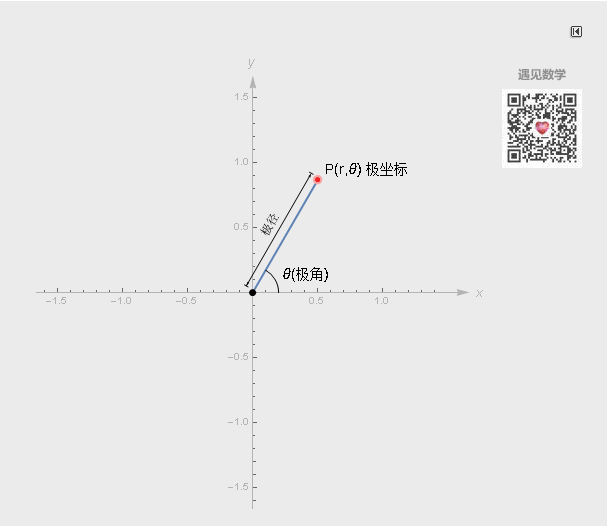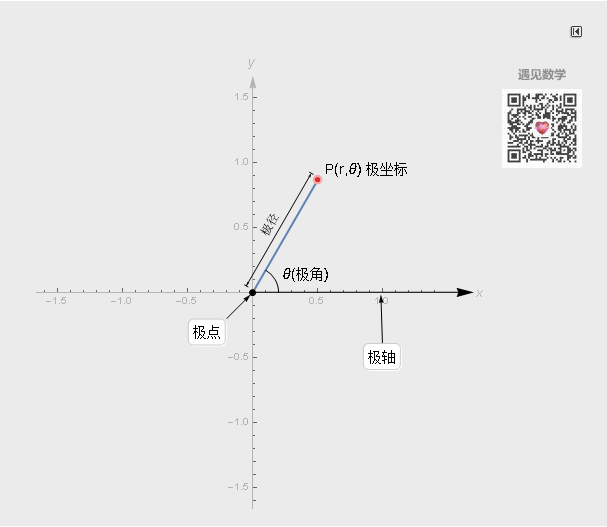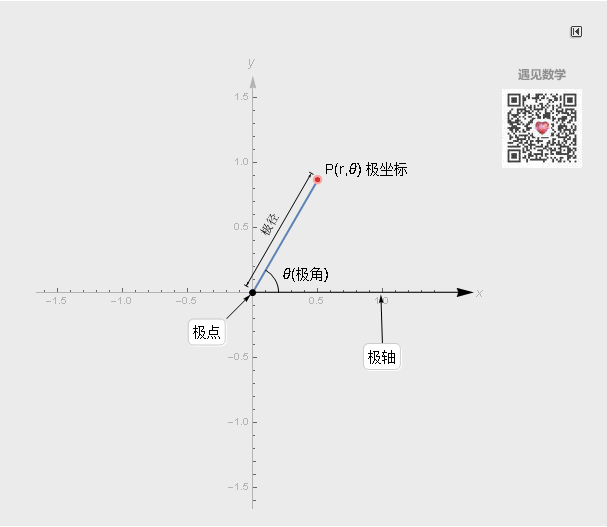
极坐标中的点
极坐标系也有两个坐标轴: r(极径)和θ (极角或角坐标),有了 r 和

极坐标系中一个重要的特性是, 平面直角坐标中的任意一点, 可以在极坐标系中有无限种表达形式. 通常来说, 点(r, θ)可以任意表示为(r, θ ±