(原创)方差标准差、六西格玛与风险
2012-01-14 12:10阅读:
连自己都很奇怪怎么把这三个概念联系在一起了:方差、标准差,统计学的概念;六西格玛,一种管理思想;风险,这里只谈公司理财中的风险衡量。所谓的“灵光一闪”就是这样吧,打开思路,开放视野,说不定能找到些它们之间的联系。
先来看方差和标准差
方差是各个数据与平均数之差的平方的平均数。在
概率论和数理统计中,方差(英文Variance)用来度量
随机变量和其数学期望(即均值)之间的偏离程度。标准差就是对方差进行开方,用
σ表示。方差和标准差都用来衡量数据或样本离中心的或围绕平均数的波动程度。样本方差或样本标准差越大,样本数据的波动就越大。
标准差也是一种平均数(方差再开方)。
这里示范如何计算一组数的标准差。例如一群孩童年龄的数值为 { 5, 6, 8, 9 }
:
第一步,计算平均值 ︰计算得出
7为平均值
第二步,计算标准差︰计算得出σ=1.5811
简单来说,标准差是一组数值自平均值 分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
在实际应用上,常考虑一组数据具有近似于正态分布的机率分布。若其假设正确,则约
68% 数值分布在距离平均值有 1 个标准差之内的范围,约 95% 数值分布在距离平均值有 2 个标准差之内的范围,以及约 99.7%
数值分布在距离平均值有 3 个标准差之内的范围。称为 '68-95-99.7法则'。
六西格玛
上面我们提到,“西格玛”指标准差,从统计学角度讲,六西格玛代表什么呢?我们先来看1个西格玛的含义:在标准正态分布表中,1个西格玛表示数据在平均数正负1个标准差范围内的概率是68.26%,2个西格玛表示数据在平均数正负两个标准差范围内的概率约为95%。。。。。。6个西格玛则表示数据落在平均数正负6个标准差的概率约为99.99966%!
六西格玛最先用在质量改进控制方法中,是一个过程性能的指标,表示
每一百万活动或每一百万产品中,3.4个(次数)不合格。其数理统计学意义是:一个过程如果具有
6σ的能力,就意味着过程平均值与规格上下限的控制距离为6σ的标准偏差。这时,过程具有非常好的质量特性,即一百万个过程数据仅有3.4个落在规格上下线以外,基本上接近零的不合格。这是近乎完美的一个标准。所以,从这个角度理解,我们可以把6西格玛作为一种管理上的最高标准(质量水平、流程性能等)。
我们经常用百分比来衡量数据,比如,医生开100次处方,有1次出错,则错误率为1%,正确率为99%,我们已经认为很好了,但我们放大到
100万次来看,那么在100万次处方中,则有10000次开错!这是很惊人的数据。如果达到六西格玛标准,我们可以说,在一百万次处方中,只有3.34次开错。如果我们是患者,您希望哪个更好呢?这,就是六西格玛的魅力。当然,如何达到这个标准,六西格玛又提供了很多的工具和方法,其中DMAIC模式为主要工具,我们专文再谈。从这个角度讲,六西格玛又是一种管理流程、管理思想和管理工具。
一个比较困惑的地方是,从统计学角度讲,西格玛越大,波动越大,是不好的,但在管理上的六西格玛为什么又是非常完美的一个标准呢?我们可以从另一个角度来理解,即把6σ对应的数据出现概率99.99966%作为我们的一个高标准和严要求。这里只是借用了6σ这样的一个概念,来衡量我们对工作的要求,比如99.99966%的产品合格率、99.99966%的客户满意度等等。99.99966%的合格率也就意味着产品的质量波动、客户满意度波动非常非常小。
风险
在投资管理中,风险即意味着不确定性。一般投资者是风险厌恶型的,标准差就很好地衡量了这种风险。从这个角度,标准差是衡量风险程度的一个指标。
标准差在投资决策中的应用[1]
投资是企业生产经营和发展壮大的必要手段。投资者作出
投资决策时,不仅要考虑预期回报,还必须分析比较
投资风险。
由于投资风险的客观存在性及其对
投资收益的不利性,投资者在进行投资决策时必须而且也应该对投资风险进行分析,尽可能地测定和量化风险的大小。
1、用标准差衡量风险大小。此时的标准差计算公式如下:
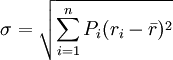
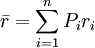
其中
σ为标准差,
Pi为期望投资收益率,
Pi为一系列可能性事件发生的概率,
ri为可能性事件发生时的
投资收益。标准差值越小,说明投资风险越小。
假设投资者要在A、B两个项目中选择一个或两个项目进行投资。估计第二年每个项目的
收益率可能有四个结果,每个结果都有一个确定的概率与之对应。如下表所示,表中r为收益率,p为收益率实现的可能性。
表1 A、B两项目的收益率分布
-
|
A项目 |
B项目 |
| r |
p |
r |
p |
| 1 |
0.2 |
0.25 |
1.0 |
0.05 |
| 2 |
0.14 |
0.25 |
0.6 |
0.2 |
| 3 |
0.10 |
0.25 |
0.1 |
0.7 |
| 4 |
0.04 |
0.25 |
-1.0 |
0.05 |
投资项目A、B的
期望收益率分别为:
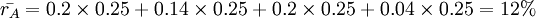
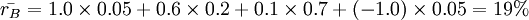
计算结果表明,A项目的
期望收益率小于B项目。但从
收益率的分布看,A项目的收益率在4%~20%之间波动,变动范围小;而B项目收益率从-100%到+100%,变动范围大。收益率的变动大小反映了风险的大小,收益率变动大,风险就大。根据公式(3)计算得:
σA
= 5.83%,
σB =
37.80%。这是不是说明B项目的风险更大呢?从数学角度看,B项目标准差大可能来源于B项目的各种可能收益都比较大。
2、标准差的局限性。当不同项目的期望回报率相同时,用标准差衡量风险程度是合适的,否则就不能再用标准差而必须用一个相对的
风险指标。取标准差与期望值的比率
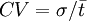
;,称为
变异系数或标准离差,该值越大反映项目的风险越大。
可以计算项目A的变异系数
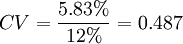
,项目B的变异系数
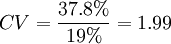
。这个时候就可以说B项目风险更大。
风险与六西格玛
除了投资风险,在公司经营管理中,我们还会面临很多的风险,内控风险、市场风险、生产质量风险、人员管理风险等等,面对这些风险,我们可以借用六西格玛相关工具来帮助我们把风险控制在可以接受的范围内。

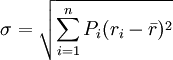
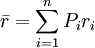
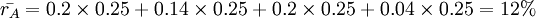
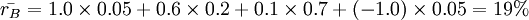
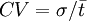 ;,称为
;,称为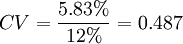 ,项目B的变异系数
,项目B的变异系数 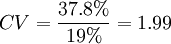 。这个时候就可以说B项目风险更大。
。这个时候就可以说B项目风险更大。