浅谈C++ STL库 RB树 AVL树

2011-06-04 20:59阅读：

http://blog.sina.cn/dpool/blog/u/1993399317

C++ STL 之所以得到广泛的赞誉，也被很多人使用，不只是提供了像vector, string, list等方便的容器，更重要的是STL封装了许多复杂的数据结构算法和大量常用数据结构操作。vector封装数组，list封装了链表，map和 set封装了二叉树等，在封装这些数据结构的时候，STL按照程序员的使用习惯，以成员函数方式提供的常用操作，如：插入、排序、删除、查找等。让用户在 STL使用过程中，并不会感到陌生。
C++ STL中标准关联容器set, multiset, map, multimap内部采用的就是一种非常高效的平衡检索二叉树：红黑树，也成为RB树(Red-Black Tree)。RB树的统计性能要好于一般的平衡二叉树(有些书籍根据作者姓名，Adelson-Velskii和Landis，将其称为AVL-树)，所以被STL选择作为了关联容器的内部结构。本文并不会介绍详细AVL树和RB树的实现以及他们的优劣，关于RB树的详细实现参看红黑树: 理论与实现(理论篇)。本文针对开始提出的几个问题的回答，来向大家简单介绍map和set的底层数据结构。
为何map和set的插入删除效率比用其他序列容器高？
大部分人说，很简单，因为对于关联容器来说，不需要做内存拷贝和内存移动。说对了，确实如此。map和set容器内所有元素都是以节点的方式来存储，其节点结构和链表差不多，指向父节点和子节点。结构图可能如下：
A

/ \
B C
/ \ / \
D E F G
因此插入的时候只需要稍做变换，把节点的指针指向新的节点就可以了。删除的时候类似，稍做变换后把指向删除节点的指针指向其他节点就OK了。这里的一切操作就是指针换来换去，和内存移动没有关系。
为何每次insert之后，以前保存的iterator不会失效？
看见了上面答案的解释，你应该已经可以很容易解释这个问题。iterator这里就相当于指向节点的指针，内存没有变，指向内存的指针怎么会失效呢(当然被删除的那个元素本身已经失效了)。相对于vector来说，每一次删除和插入，指针都有可能失效，调用push_back在尾部插入也是如此。因为为了保证内部数据的连续存放，iterator指向的那块内存在删除和插入过程中可能已经被其他内存覆盖或者内存已经被释放了。即使时push_back的时候，容器内部空间可能不够，需要一块新的更大的内存，只有把以前的内存释放，申请新的更大的内存，复制已有的数据元素到新的内存，最后把需要插入的元素放到最后，那么以前的内存指针自然就不可用了。特别时在和find等算法在一起使用的时候，牢记这个原则：不要使用过期的iterator。
为何map和set不能像vector一样有个reserve函数来预分配数据？
我以前也这么问，究其原理来说时，引起它的原因在于在map和set内部存储的已经不是元素本身了，而是包含元素的节点。也就是说map内部使用的Alloc并不是map<Key, Data, Compare, Alloc>声明的时候从参数中传入的Alloc。例如：
map<int, int, less<int>, Alloc<int> > intmap;
这时候在intmap中使用的allocator并不是Alloc<int>, 而是通过了转换的Alloc，具体转换的方法时在内部通过Alloc<int>::rebind重新定义了新的节点分配器，详细的实现参看彻底学习STL中的Allocator。其实你就记住一点，在map和set内面的分配器已经发生了变化，reserve方法你就不要奢望了。
当数据元素增多时（10000和20000个比较），map和set的插入和搜索速度变化如何？
如果你知道log2的关系你应该就彻底了解这个答案。在map和set中查找是使用二分查找，也就是说，如果有16个元素，最多需要比较4次就能找到结果，有32个元素，最多比较5次。那么有10000个呢？最多比较的次数为log10000，最多为14次，如果是20000个元素呢？最多不过15次。看见了吧，当数据量增大一倍的时候，搜索次数只不过多了1次，多了1/14的搜索时间而已。你明白这个道理后，就可以安心往里面放入元素了。
最后，对于map和set Winter还要提的就是它们和一个c语言包装库的效率比较。在许多unix和linux平台下，都有一个库叫isc，里面就提供类似于以下声明的函数:
void tree_init(void **tree);
void *tree_srch(void **tree, int (*compare)(), void *data);
void tree_add(void **tree, int (*compare)(), void *data, void (*del_uar)());
int tree_delete(void **tree, int (*compare)(), void *data,void (*del_uar)());
int tree_trav(void **tree, int (*trav_uar)());
void tree_mung(void **tree, void (*del_uar)());
许多人认为直接使用这些函数会比STL map速度快，因为STL map中使用了许多模板什么的。其实不然，它们的区别并不在于算法，而在于内存碎片。如果直接使用这些函数，你需要自己去new一些节点，当节点特别多，而且进行频繁的删除和插入的时候，内存碎片就会存在，而STL采用自己的Allocator分配内存，以内存池的方式来管理这些内存，会大大减少内存碎片，从而会提升系统的整体性能。Winter在自己的系统中做过测试，把以前所有直接用isc函数的代码替换成map，程序速度基本一致。当时间运行很长时间后（例如后台服务程序），map的优势就会体现出来。从另外一个方面讲，使用map会大大降低你的编码难度，同时增加程序的可读性。何乐而不为？

RB树算法实现如下：
1、头文件 RBTree.h
1.#ifndef RBTREE__JOHN__DMRC
2.#define RBTREE__JOHN__DMRC
3.
4.template <typename T>
5.class Node{
6.public:
7. Node() : red(false), exist(false), left(NULL), right(NULL), parent(NULL){}
8. Node(T &t) : data(t), red(true), exist(true), left(NULL), right(NULL), parent(NULL){}
9. //function 10. // max & min 11. Node<T>* maximum();
12. Node<T>* minimum();
13. // successor & predecessor 14. Node<T>* successor();
15. Node<T>* predecessor();
16. // exist 17. bool isExist() { return this ->exist; }
18. bool isNULL() { return !this ->exist; }
19. // red & black ( black = 0 & red = 1 ) 20. bool getColor() { return this ->red; }
21. bool isRed(){ return this ->red; }
22. bool isBlack() { return !this ->red; }
23. void setColor(bool c) { this ->red = c; }
24. void setRed() { this ->red = true; }
25. void setBlack() { this ->red = false; }
26. //varables
27. T data;
28. bool red;
29. bool exist;
30. Node<T>* left;
31. Node<T>* right;
32. Node<T>* parent;
33.};
34.
35.
36.template <typename T, typename E>
37.class RBTree{
38.public:
39. RBTree() : root(NULL){}
40. ~RBTree();
41. bool Insert(T &);
42. bool Delete(T &, E);
43. // debug 44. T get_head(){ return root ->data;}
45.private:
46. // delete_tree; 47. void delete_tree(Node<T>*);
48. // delete a node; 49. bool delete_node(T&, Node<T>*);
50. // rotates 51. void left_rotate(Node<T>*);
52. void right_rotate(Node<T>*);
53. // fixups 54. void insert_fixup(Node<T>*);
55. void delete_fixup(Node<T>*);
56. Node<T>* root;
57.};
58.
59.#endif 2、实现 RBTree.cpp
1.#include 'RBTree.h'
2.
3.template <typename T>
4.Node<T>* Node<T>::maximum(){
5. Node<T>* x = this;
6. while(x ->right ->isExist())
7. x = x ->right;
8. return x;
9.}
10.11.template <typename T>
12.Node<T>* Node<T>::minimum(){
13. Node<T>* x = this;
14. while(x ->left ->isExist())
15. x = x ->left;
16. return x;
17.}
18.
19.template <typename T>
20.Node<T>* Node<T>::successor(){
21. Node<T>* y;
22. Node<T>* x;
23. if(this ->right ->isExist())
24. return this ->right ->minimum();
25. x = this;
26. y = x ->parent;
27. while(y != NULL && x == y ->right){
28. x = y;
29. y = x ->parent;
30. }
31. return y;
32.}
33.
34.template <typename T>
35.Node<T>* Node<T>::predecessor(){
36. Node<T>* y;
37. Node<T>* x;
38. if(this ->left ->isExist())
39. return this ->left ->maximum();
40. x = this;
41. y = x ->parent;
42. while(y != NULL && x == y ->left){
43. x = y;
44. y = x ->parent;
45. }
46. return y;
47.}
48.
49.template <typename T, typename E>
50.RBTree<T, E>::~RBTree(){
51. this ->delete_tree(this ->root);
52.}
53.54.template <typename T, typename E>
55.void RBTree<T, E>::delete_tree(Node<T>* p){
56. if(p){
57. if(p ->left)
58. this ->delete_tree(p ->left);
59. if(p ->right)
60. this ->delete_tree(p ->right);
61. delete p;
62. }
63.}
64.
65.// Insert & fixup 66.template <typename T, typename E>
67.bool RBTree<T, E>::Insert(T &t){
68. if(this ->root == NULL || this ->root ->isNULL()){
69. if(this ->root)
70. delete this ->root;
71. this ->root = new Node<T>(t);
72. this ->root ->left = new Node<T>();
73. this ->root ->left ->parent = this ->root;
74. this ->root ->right = new Node<T>();
75. this ->root ->right ->parent = this ->root;
76. this ->root ->setBlack();
77. return true;
78. }
79. Node<T>* p = this ->root;
80. while(1){
81. if(t == p ->data)
82. return false;
83. if(t < p ->data){
84. if(p ->left ->isNULL()){
85. delete p ->left;
86. p ->left = new Node<T>(t);
87. p ->left ->parent = p;
88. p ->left ->left = new Node<T>();
89. p ->left ->left ->parent = p ->left;
90. p ->left ->right = new Node<T>();
91. p ->left ->right ->parent = p ->left;
92. this ->insert_fixup(p ->left);
93. return true;
94. }
95. else96. p = p ->left;
97. }
98. else{
99. if(p ->right ->isNULL()){
100. delete p ->right;
101. p ->right = new Node<T>(t);
102. p ->right ->parent = p;
103. p ->right ->left = new Node<T>();
104. p ->right ->left ->parent = p ->left;
105. p ->right ->right = new Node<T>();
106. p ->right ->right ->parent = p ->left;
107. this ->insert_fixup(p ->right);
108. return true;
109. }
110. else111. p = p ->right;
112. }
113. }
114. return false;
115.}
116.
117.template <typename T, typename E>
118.void RBTree<T, E>::insert_fixup(Node<T>* z){
119. Node<T>* y;
120.121. while(z ->parent && z ->parent ->isRed()){
122. if(z ->parent == z ->parent ->parent ->left){
123. y = z ->parent ->parent ->right;
124. if(y ->isRed()){
125. //case 1 126. z ->parent ->setBlack();
127. y ->setBlack();
128. z ->parent ->parent ->setRed();
129. z = z ->parent ->parent;
130. }
131. else{
132. if(z == z ->parent ->right){
133. // case 2 ( fall through to case 3 ) 134. z = z ->parent;
135. this ->left_rotate(z);
136. }
137. // case 3 138. z ->parent ->setBlack();
139. z ->parent ->parent ->setRed();
140. this ->right_rotate(z ->parent ->parent);
141. }
142. }
143. else{
144. y = z ->parent ->parent ->left;
145. if(y ->isRed()){
146. // case 4 147. z ->parent ->setBlack();
148. y ->setBlack();
149. z ->parent ->parent ->setRed();
150. z = z ->parent ->parent;
151. }
152. else{
153. if(z == z ->parent ->left){
154. // case 5 ( fall through to case 6 ) 155. z = z ->parent;
156. this ->right_rotate(z);
157. }
158. // case 6 159. z ->parent ->setBlack();
160. z ->parent ->parent ->setRed();
161. this ->left_rotate(z ->parent ->parent);
162. }
163. }
164. }
165. this ->root ->setBlack();
166.}
167.// delete & fixup 168.template <typename T, typename E>
169.bool RBTree<T, E>::Delete(T &t, E e){
170. Node<T>* p = this ->root;
171. while(p ->isExist()){
172. if(p ->data == e)
173. return this ->delete_node(t, p);
174. else if(e < p ->data)
175. p = p ->left;
176. else177. p = p ->right;
178. }
179. return false;
180.}
181.
182.template <typename T, typename E>
183.bool RBTree<T, E>::delete_node(T& t, Node<T>* z){
184. Node<T>* y;
185. Node<T>* x;
186.
187. if(z ->left ->isNULL() || z ->right ->isNULL())
188. y = z;
189. else190. y = z ->successor();
191. if(y ->left ->isExist()){
192. x = y ->left;
193. if(y ->right ->isNULL())
194. delete y ->right;
195. }
196. else{
197. x = y ->right;
198. if(y ->left ->isNULL())
199. delete y ->left;
200. }
201. x ->parent = y ->parent;
202. if(y ->parent == NULL)
203. this ->root = x;
204. else if(y == y ->parent ->left)
205. y ->parent ->left = x;
206. else207. y ->parent ->right = x;
208. if(y != z){
209. T temp = z ->data;
210. z ->data = y ->data;
211. y ->data = temp;
212. }
213. if(y ->isBlack())
214. this ->delete_fixup(x);
215. t = y ->data;
216.
217. delete y;
218.
219. return true;
220.}
221.222.template <typename T, typename E>
223.void RBTree<T, E>::delete_fixup(Node<T>* x){
224. Node<T>* w;
225. while(x != this ->root && x ->isBlack()){
226. if(x == x ->parent ->left){
227. w = x ->parent ->right;
228. if(w ->isRed()){
229. // case 1 ( fall through ) 230. w ->setBlack();
231. x ->parent ->setRed();
232. this ->left_rotate(x ->parent);
233. w = x ->parent ->right;
234. }
235. if(w ->left ->isBlack() && w ->right ->isBlack()){
236. // case 2 ( new circle with x's value changed ) 237. w ->setRed();
238. x = x ->parent;
239. }
240. else{
241. if(w ->right ->isBlack()){
242. // case 3 ( fall through to case 4 ) 243. w ->left ->setBlack();
244. w ->setRed();
245. this ->right_rotate(w);
246. w = x ->parent ->right;
247. }
248. // case 4 ( exit the while with x = root ) 249. w ->setColor(x ->parent ->getColor());
250. x ->parent ->setBlack();
251. w ->right ->setBlack();
252. this ->left_rotate(x ->parent);
253. x = this ->root;
254. }
255. }
256. else{
257. w = x ->parent ->left;
258. if(w ->isRed()){
259. // case 5 ( fall through ) 260. w ->setBlack();
261. x ->parent ->setRed();
262. this ->right_rotate(x ->parent);
263. w = x ->parent ->left;
264. }
265. if(w ->left ->isBlack() && w ->right ->isBlack()){
266. // case 6 ( new circle with x's value changed ) 267. w ->setRed();
268. x = x ->parent;
269. }
270. else{
271. if(w ->left ->isBlack()){
272. // case 7 ( fall through to case 8 ) 273. w ->right ->setBlack();
274. w ->setRed();
275. this ->left_rotate(w);
276. w = x ->parent ->left;
277. }
278. // case 8 ( exit the while with x = root) 279. w ->setColor(x ->parent ->getColor());
280. x ->parent ->setBlack();
281. w ->left ->setBlack();
282. this ->right_rotate(x ->parent);
283. x = this ->root;
284. }
285. }
286. }
287. x ->setBlack();
288.}
289.
290.// rotate 291.template <typename T, typename E>
292.void RBTree<T, E>::left_rotate(Node<T>* x){
293. Node<T>* y = x ->right;
294. // set beta 295. x ->right = y ->left;
296. if(y ->left)
297. y ->left ->parent = x;
298. // set parent 299. y ->parent = x ->parent;
300. if(x ->parent == NULL)
301. this ->root = y;
302. else{
303. if(x == x ->parent ->left)
304. x ->parent ->left = y;
305. else306. x ->parent ->right = y;
307. }
308. // set relation 309. y ->left = x;
310. x ->parent = y;
311.}
312.313.template <typename T, typename E>
314.void RBTree<T, E>::right_rotate(Node<T>* x){
315. Node<T>* y = x ->left;
316. // set beta 317. x ->left = y ->right;
318. if(y ->right)
319. y ->right ->parent = x;
320. // set parent 321. y ->parent = x ->parent;
322. if(x ->parent == NULL)
323. this ->root = y;
324. else{
325. if(x == x ->parent ->left)
326. x ->parent ->left = y;
327. else328. x ->parent ->right = y;
329. }
330. // set relation 331. y ->right = x;
332. x ->parent = y;
333.}
334.
3、简单的应用 main.cpp

1.#include <iostream>
2.#include <string>
3.
4.template<typename T, typename E> class RBTree;
5.
6.using namespace std;
7.
8.int main(void){
9. RBTree<int, int> s;
10. int i, a[10] = { 1, 2, 3, 4, 6, 8, 0, 7, 5, 9};
11. for(i = 0; i < 10; i ++){
12. s.Insert(a[i]);
13. cout << s.get_head() << endl;
14. }
15. return 0;
16.17.}

什么是AVL树
AVL 树是一种二叉排序树，但是它能保持自身的高度平衡，这使得的树的查找与插入都很快，当然为了维持树的平衡在树节点插入与删除过程中也要做一些维持树本身平衡的操作。AVL树是由前苏联人G.M. Adelson-Velskii and E.M. Landis 1962年共同发明的，这种结构是计算机科学中发明的第一个有自平衡特性的数据结构，有着开创意义，为后来发明的2-4树、红黑树，AA树等指出了方向，这种设计思想有着很重要的意义。因为后来设计的更加复杂的数据结构如红黑树在平均性能上超过了AVL树，因此AVL树直接应用场合己不多见，但是学习它其中的优秀设计思想对提高自己的水平还是有很重要的意义，如果想了解红黑树可以查看我以前写的一篇关于红黑树的日志，地址如下：
http://saturnman.blog.163.com/blog/static/5576112010969420383/
本文是我在知道什么时候是AVL树后自己推导树的插入与删除算法的，整个算法和代码都没见得优雅和有效率，写这个总结只是为了练习自己的分析数据结构的能力，如果读本人者想找一种优雅而高效的实现，那请自行google查寻之。
1. AVL树定义：
  1. 树是一棵二叉查找树
  2. 定义树的平衡因子为右子树的高度减去左子树的高度，那么树的平衡因子只能为-1 0 或1。

AVL树实现算法
#include<iostream>
#include<iomanip>
using namespace std;

class linknod;
class avl
{
friend class linknod;
public:
avl();
int instalnod(int);//插入结点函数
int deletnod(int);//删除结点函数
int findnod(int,linknod*);//查找结点函数
void pushs(linknod*);//结点路径入栈
linknod* pope();//结点路径出栈
void subll(linknod*);//左旋二叉树
void sublr(linknod*);//先左后右旋转
void subrr(linknod*);//右旋二叉数
void subrl(linknod*);//先右后左旋
void display(linknod*);
void displaym(linknod*);
linknod *ptr;//根结点指针
linknod *first;
private:
linknod *subl;//右旋指针
linknod *subr;//左旋指针
linknod* stacts[100];//路径查找结点存储栈
int top;//栈顶指针
int botem;//栈低指针
};
class linknod
{
friend class avl;
public:
linknod();
private:
int bf;//平衡因子
int data;
linknod *lchild;
linknod *rchild;
linknod *perint;
};
avl::avl()
{
subl=0;
subr=0;
ptr=0;
top=-1;
botem=-1;
for(int i=0;i<100;i++)
stacts[i]=0;
}
linknod::linknod()
{
perint=0;
lchild=0;
rchild=0;
data=0;
bf=0;
}
void avl::display(linknod* n)
{
if(n!=0)
{
cout<<n->data<<' ';
display(n->lchild);
display(n->rchild);
}
}
void avl::displaym(linknod*n)
{
if(n!=0)
{
displaym(n->lchild);
cout<<n->data<<' ';
displaym(n->rchild);
}
}
void avl::pushs(linknod* n)
{
botem=-1;
top++;
stacts[top]=n;
}
linknod* avl::pope()
{
linknod* n;
botem=-1;
n=stacts[top];
top--;
return n;
}
int avl::deletnod(int n)
{
linknod *pr=0,*p=ptr,*q,*ppr;
int d,dd=0,tag=0,tag1=0;
top=-1;//初始化栈顶指针
while(p!=0)//查找要删除的结点并记录查找路径
{
if(n==p->data)
break;
pr=p;
pushs(pr);
if(n<p->data)
p=p->lchild;
else
p=p->rchild;
}
if(p==0)
return -1;
if(p->lchild!=0&&p->rchild!=0)
{
pr=p;
pushs(pr);
q=p->lchild;
while(q->rchild!=0)
{
pr=q;
pushs(pr);
q=q->rchild;
}
p->data=q->data;
p=q;
}
if(p->lchild!=0)
q=p->lchild;
else
{
q=p->rchild;
}
if(pr==0)
ptr=q;
else
{
if(pr->lchild==p)
{
pr->lchild=q;
if(pr->lchild!=0)//
pr->lchild->perint=pr;
tag=1;
}
else
{
pr->rchild=q;
if(pr->rchild!=0)
pr->rchild->perint=pr;
tag1=1;
}
while(top!=botem)
{
pr=pope();
if(pr->lchild!=0||pr->rchild!=0)
{
if(pr->rchild==q)
{
pr->bf--;
}
if(pr->lchild==q)
{
pr->bf++;
}
}
else
{
if(tag==1)
{
pr->bf++;
tag=0;
}
if(tag1==1)
{
pr->bf--;
tag1=0;
}
}
if(pr->bf==1||pr->bf==-1)
break;
if(pr->bf!=0)
{
if(pr->bf<0)
{
d=-1;
q=pr->lchild;
}
else
{
d=1;
q=pr->rchild;
}
if(q->bf==0)
{
if(d==-1)
{
subrr(pr);
}
else
{
subll(pr);
}
break;
}
if(q->bf==d)
{
if(d==-1)
subrr(pr);
else
subll(pr);
}
else
{
if(d==-1)
sublr(pr);
else
subrl(pr);//
}
}
q=pr;
}
}
delete p;
return 1;
}
int avl::findnod(int n,linknod* t)
{
int tag=0;
while(t!=0)
{
if(n<t->data)
t=t->lchild;
else
{
if(n>t->data)
t=t->rchild;
else
if(n==t->data)
{
tag=1;
break;
}
}
}
if(tag!=1)
return 0;
else
return 1;
}
int avl::instalnod(int n)
{
linknod *p=0;
linknod *pr=0;
linknod *r=0;
int d;
p=ptr;
while(p!=0)
{
if(n==p->data)
{
return -1;
}
pr=p;
pushs(pr);//存储查找路径
if(n<p->data)//根据插入至的大小判断插入位置
p=p->lchild;
else
p=p->rchild;
}
p=new linknod;
p->data=n;
p->bf=0;
if(ptr==0)
{
ptr=p;
first=p;
p->perint=0;
return 1;
}
p->perint=pr;
if(n<pr->data)
pr->lchild=p;
else
pr->rchild=p;
while(top!=botem)
{
linknod *temp;
temp=pope();
if(p==temp->lchild)
temp->bf--;
else
temp->bf++;
if(temp->bf==0)
{
top=-1;
break;
}
if(temp->bf==1||temp->bf==-1)
{
p=temp;
}
if(temp->bf==2||temp->bf==-2)
{
top=-1;//初始化栈顶指针
d=(temp->bf<0)?-1:1;
if(p->bf==d)
{
if(d==-1)
{
subrr(temp);
}
else
{
subll(temp);
}
}
else
{
if(d==-1)
{
sublr(temp);
}
else
subrl(temp);
}
break;
}
}
}
void avl::subll(linknod* n)//已修改完善
{
int tag=0,flag1=0;
subl=n;
n=subl->rchild;
if(subl!=first)
tag=1;
subl->rchild=n->lchild;
if(subl->rchild!=0)
{
subl->rchild->perint=subl;
flag1=1;
}
n->lchild=subl;
if(subl->perint!=0)
{
if(subl->perint->data>subl->data)
{
subl->perint->lchild=n;
}
else
{
subl->perint->rchild=n;
}
n->perint=subl->perint;
}
else
{
n->perint=0;
}
subl->perint=n;
ptr=n;
if(tag==1)
{
ptr=first;
tag=0;
}
else
{
first=ptr;
ptr->perint=0;
}
if(flag1==1)
{
subl->bf=1;
n->bf=-1;
flag1=0;
}
else
{
subl->bf=0;
n->bf=0;
}
}
void avl::subrr(linknod* n)//修改完善
{
int tag=0,flag1=0;
subr=n;
n=subr->lchild;
if(subr!=first)
tag=1;
subr->lchild=n->rchild;
if(subr->lchild!=0)
{
subr->lchild->perint=subr;
flag1=1;
}
n->rchild=subr;
if(subr->perint!=0)
{
if(subr->perint->data>subr->data)
{
subr->perint->lchild=n;
}
else
{
subr->perint->rchild=n;
}
n->perint=subr->perint;
}
else
{
n->perint=0;
}
subr->perint=n;
ptr=n;
if(tag==1)
{
ptr=first;
tag=0;
}
else
{
first=ptr;
ptr->perint=0;
}
if(flag1==1)
{
subr->bf=-1;
n->bf=1;
flag1=0;
}
else
{
n->bf=0;
subr->bf=0;
}
}
void avl::sublr(linknod* n)//已修改好
{
int tag=0;
subr=n;
subl=subr->lchild;
n=subl->rchild;
if(subr!=first)
tag=1;
subl->rchild=n->lchild;
if(subl->rchild!=0)
subl->rchild->perint=subl;
n->lchild=subl;
subl->perint=n;
if(n->bf<=0)
subl->bf=0;
else
subl->bf=-1;
subr->lchild=n->rchild;
if(subr->lchild!=0)
subr->lchild->perint=subr;
n->rchild=subr;
if(subr->perint!=0)
{
if(subr->perint->data<subr->data)
{
subr->perint->rchild=n;
}
else
{
subr->perint->lchild=n;
}
n->perint=subr->perint;
}
if(n->bf==-1)
subr->bf=1;
else
subr->bf=0;
subr->perint=n;
ptr=n;
if(tag==1)
{
ptr=first;
tag=0;
}
else
{
first=ptr;
ptr->perint=0;
}
n->bf=0;
}
void avl::subrl(linknod* n)//修改好
{
int tag=0;
subl=n;
subr=subl->rchild;
n=subr->lchild;
if(subl!=first)
tag=1;
subr->lchild=n->rchild;
if(subr->lchild!=0)
subr->lchild->perint=subr;
n->rchild=subr;
subr->perint=n;
if(n->bf>=0)
subr->bf=0;
else
subr->bf=1;
subl->rchild=n->lchild;
if(subl->rchild!=0)
subl->rchild->perint=subl;
n->lchild=subl;
if(subl->perint!=0)
{
if(subl->perint->data<subl->data)
{
subl->perint->rchild=n;
}
else
{
subl->perint->lchild=n;
}
n->perint=subl->perint;
}
if(n->bf==1)
subl->bf=-1;
else
subl->bf=0;
subl->perint=n;
ptr=n;
if(tag==1)
{
ptr=first;
tag=0;
}
else
{
first=ptr;
ptr->perint=0;
}
n->bf=0;
}
int main()
{
char select[100],slt; avl mm;
int num[1000],m=0,n=0,n1=0,total=0,t=0,tag=0,ll=0,ll2=0,f=0;
cout<<' AVL树操作菜单'<<endl;
cout<<'***********************************'<<endl;
cout<<' 1.建立平衡二叉树'<<endl;
cout<<' 2.插入结点 '<<endl;
cout<<' 3.删除结点 '<<endl;
cout<<' 4.查找结点 '<<endl;
cout<<' 5.显示当前树 '<<endl;
cout<<' 6.退出 '<<endl;
cout<<'***********************************'<<endl;
cout<<'提示：本系统只能对数字进行相应操作！！！'<<endl<<endl;
cout<<'请输入要执行的功能代号：';
while(cin>>select)
{
if(!strcmp(select,'1'))
{
if(f==1)
{
cout<<'已存在一棵非空树！！若重新建树会造成已有的数据丢失！确定要重新建立吗？(y/n)'<<endl;
cin>>slt;
if(slt=='y'||slt=='Y')
f=0;
}
if(slt=='y'||slt=='Y'||f==0)
{
f=1;
mm.ptr=0;
cout<<'请输入要建立平衡二叉树的结点个数：';
cin>>n;
n=ll+n;
cout<<'请输入要建立平衡二叉树的结点'<<endl;
for(int i=0;i<n;i++)
cin>>num[i];
for(int i=0;i<n;i++)
{
if(mm.instalnod(num[i])==-1)
{
cout<<'结点 '<<num[i]<<' 已存在！！！'<<endl;
n--;
continue;
}
}
cout<<'前序遍历'<<endl;
mm.display(mm.ptr);
cout<<endl<<'中序遍历'<<endl;
mm.displaym(mm.ptr);
cout<<endl;
tag=0;
}
}
else
{
if(!strcmp(select,'2'))
{
cout<<'请输入要插入的结点个数：'<<endl;
cin>>n1;
n1=ll2+n1;
cout<<'请输入要插入的结点'<<endl;
for(int i=0;i<n1;i++)
{
cin>>num[i];
}
for(int i=0;i<n1;i++)
{
if(mm.instalnod(num[i])==-1)
{
cout<<'结点 '<<num[i]<<' 已存在！！！'<<endl;
n1--;
continue;
}
}
cout<<'前序遍历'<<endl;
mm.display(mm.ptr);
cout<<endl<<'中序遍历'<<endl;
mm.displaym(mm.ptr);
cout<<endl;
tag=0;
}
else
{
if(!strcmp(select,'3'))
{
if(tag==0)
{
total=n+n1;
tag=1;
}
if(total==0)
{
cout<<'此树为空树，请新建一棵树！！！'<<endl;
}
else
{
cout<<'请输入要删除的结点值:';
cin>>m;
t=mm.deletnod(m);
if(t==1)
total--;
else
{
cout<<'没有要删除的结点！！！'<<endl;

}
if(total!=0)
{
cout<<'前序遍历'<<endl;
mm.display(mm.ptr);
cout<<endl<<'中序遍历'<<endl;
mm.displaym(mm.ptr);
cout<<endl;
}
else
{
cout<<'此树已删空!!!!'<<endl;
total=0;
n=0;n1=0;
f=0;
}
}
}
else
{
if(!strcmp(select,'4'))
{
cout<<'请输入要查找的结点：' <<endl;
cin>>m;
if(mm.findnod(m,mm.ptr)==1)
{
cout<<'存在要查的结点'<<m<<'!!'<<endl;
}
else
{
cout<<'结点'<<m<<'不存在!!'<<endl;
}
}
else
{
if(!strcmp(select,'5'))
{
if(mm.ptr!=0)
{
cout<<'前序遍历'<<endl;
mm.display(mm.ptr);
cout<<endl<<'中序遍历'<<endl;
mm.displaym(mm.ptr);
cout<<endl;
}
else
{
cout<<'此树为空树！！！'<<endl;
f=0;
}
}
else
{
if(!strcmp(select,'6'))
{
exit(1);
}
else
{
cout<<'输入的选项非法！请正确输入！'<<endl;
}
}
}
}
}
}
cout<<endl<<' AVL树操作菜单'<<endl;
cout<<'***********************************'<<endl;
cout<<' 1.建立平衡二叉树'<<endl;
cout<<' 2.插入结点 '<<endl;
cout<<' 3.删除结点 '<<endl;
cout<<' 4.查找结点 '<<endl;
cout<<' 5.显示当前树 '<<endl;
cout<<' 6.退出 '<<endl;
cout<<'***********************************'<<endl;
cout<<'提示：本系统只能对数字进行相应操作！！！'<<endl<<endl;
cout<<'请输入要执行的功能代号：';
}
}

平衡二叉树（这里就不解释了）：给予不同的平衡条件，造就出不同的效率表现，以及不同的实现复杂度，AVL ，RB， AA都是一种平衡二叉树，因为维护平衡，所以插入和删除节点的平均时间长了，但是可以避免不平衡的情况，所以元素的搜寻访问时间短了！而最直观的平衡条件是整棵树的深度为logN，也就是说要求每个节点的左右子树有相同的高度（递归定义的结果就是该树的叶子节点都在同一层上！）
接下来是AVL树： AVL树，原名是Adelson-Velskii-Landis tree，它没有像上述那个条件要求那么苛刻，它允许任何节点的左右子树的高度相差1，（递归定义的结构就是该树的叶子节点只可以在最后一层和倒数第二层）
下面分析“插入节点”情况下几种使得AVL树不平衡的情况以及解决方法
一旦插入节点后，AVL树不平衡，只要调整“插入点到根节点”的那条路径上，平衡状态被破坏的所有节点中最深的那个，就可以使得整棵树重新获得到平衡，假设该节点为X，

clip_image002

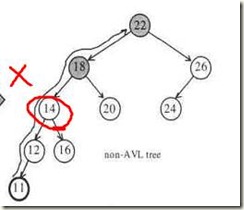
那么有以下四种情况
1 插入点位于X 的左子节点的左子树 ----左左（外侧）//不管是在左子树的什么位置上插入
2 插入点位于X的左子节点的右子树 -- 左右（内侧）
3 插入点位于X的右子节点的左子树（外侧）
4 插入点位于X的右子节点的右子树（内侧）

clip_image004

在外侧插入—也就是在完成外侧插入后，某个顶点成为第一个违反平衡条件，是下面这种状态（违反点为k2）也就是情况【1】【4】
1 插入点位于X 的左子节点的左子树 ----左左（外侧）
4 插入点位于X的右子节点的右子树（内侧）

clip_image006

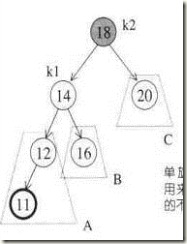
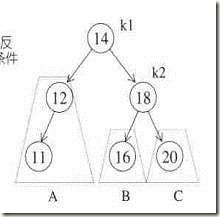
插入11后，使得A子树成长了一层，但是这样并不会让k1树不平衡，但是A子树的深度却比C子树的深度多2，也就使得k2的左子树的高度为3，k2的右子树的高度为1，破坏了平衡。而且这种情况下，B子树不可能和A子树同层，不然的话早就不平横了，同时B子树也不可能和C子树同层，不然的话第一个违反平衡条件的就是k1而不是k2了。
我们希望A子树向上提，而C子树下降一层，可以从图里这样想象，只需要把K1向上提，而K2自然下滑，并且把B子树挂到K2的左侧，就完成了这个过程（因为本身AVL是一颗平衡二叉树，子树有一定的大小关系，所以这样操作可以得到正确的结果）右右插入的时候同理！

clip_image008

在内侧插入 – 也就是在情况【2】,【3】
2 插入点位于X的左子节点的右子树 -- 左右（内侧）
3 插入点位于X的右子节点的左子树（外侧）

clip_image010

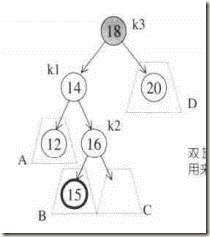
这次我们没办法对k1和k3只进行一次旋转，使得k1为根节点来完成平衡。我们可以考虑用k2节点来作为平衡树的根，这就需要两次旋转

clip_image012

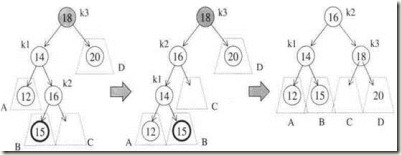
对照着上述的旋转方法，给出基本的旋转操作（暂时不考虑其他节点为空的情况）
Void singleRotation( Node* n,bool left) //n节点表示当前节点违反了平衡条件
{
Node *newHead;
If(left==TRUE) //新插入的节点在n的左子树
//左左,进行右上提拉节点，注意只适合左子节点的左子树，如果是左子节点的右子树，则需//要两次旋转
{
newHead = n->left;
if(newHead->right!=null)
n->left=newHead->right;
newHead->right=n;
n=newHead;
}
Else //右右，进行左上提拉节点
{
newHead = n->right;
if(newHead->left!=null)
n->right= newHead->left;
newHead->left = n;
n= newHead;
}
}
Void doubleRotation(Node* n, bool left)
{
If(left == TRUE) //新插入的节点在n的左子树
//左右，注意只适合左子节点的右子树，如果是左子节点的右子树，值需要一次旋转
{
singleRotation(n->left,false);
singleRotation(n,true);
}
Else
{
singleRotation(n->right,true);
singleRotation(n,true);
}
}

举报/Report

我的更多文章

下载客户端阅读体验更佳