新浪博客
等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
若随机变量 服从一个位置参数为
服从一个位置参数为  、尺度参数为
、尺度参数为  的概率分布,记为:
的概率分布,记为:
 等于位置参数,决定了分布的位置;其方差
等于位置参数,决定了分布的位置;其方差
 的开平方或标准差
的开平方或标准差  等于尺度参数,决定了分布的幅度。
等于尺度参数,决定了分布的幅度。
正态分布的概率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是位置参数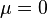 ,尺度参数
,尺度参数 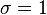 的正态分布。
的正态分布。
正态分布的概率密度函数均值为

 )是高斯函数的一个实例:
)是高斯函数的一个实例:
 .)
.)
如果一个随机变量 服从这个分布,我们写作
服从这个分布,我们写作 
 . 如果
. 如果 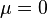 并且
并且 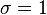 ,这个分布被称为标准正态分布,这个分布能够简化为
,这个分布被称为标准正态分布,这个分布能够简化为
正态分布中一些值得注意的量:

参考学习:维基百科
若随机变量
 服从一个位置参数为
服从一个位置参数为  、尺度参数为
、尺度参数为  的概率分布,记为:
的概率分布,记为: 等于位置参数,决定了分布的位置;其方差
等于位置参数,决定了分布的位置;其方差
 的开平方或标准差
的开平方或标准差  等于尺度参数,决定了分布的幅度。
等于尺度参数,决定了分布的幅度。正态分布的概率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是位置参数
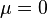 ,尺度参数
,尺度参数 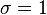 的正态分布。
的正态分布。正态分布的概率密度函数均值为


 )是高斯函数的一个实例:
)是高斯函数的一个实例: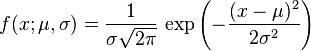 。
。
 .)
.)如果一个随机变量
 服从这个分布,我们写作
服从这个分布,我们写作 
 . 如果
. 如果 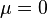 并且
并且 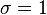 ,这个分布被称为标准正态分布,这个分布能够简化为
,这个分布被称为标准正态分布,这个分布能够简化为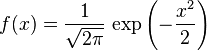 。
。
正态分布中一些值得注意的量:
- 密度函数关于平均值对称
- 平均值与它的众数(statistical mode)以及中位数(median)同一数值。
- 函数曲线下68.268949%的面积在平均数左右的一个标准差范围内。
- 95.449974%的面积在平均数左右两个标准差
 的范围内。
的范围内。 - 99.730020%的面积在平均数左右三个标准差
 的范围内。
的范围内。 - 99.993666%的面积在平均数左右四个标准差
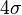 的范围内。
的范围内。 - 函数曲线的反曲点(inflection point)为离平均数一个标准差距离的位置。
参考学习:维基百科