新浪博客
.
这时，
.
,
则
.
这种情况称
与
统计独立(statistical
independence)，或 
与
独立.
与
不独立也叫
与
统计相依(statistical
dependence).也就是：P(A|B) = P(B) 或者P（A,B) =
P(A)*P(B)
多个事件互相独立：
则称
, 
, 
相互独立.
条件独立：
条件独立是条件概率的独立性，条件概率也是一种概率，只不过是将事件的空间集合改变。
设有事件R和B,当它们在事件Y定义的空间上相互独立时要满足
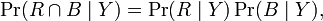
或者表达成
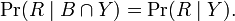
R和B在给定事件W的条件下独立时，表达为
要注意的是，X和Y独立与X和Y条件独立没有关系。显然，条件独立无法推得独立，同样的相互独立也无法保证在任意空间上条件独立。
两个事件关于某一个事件乘积的概率，等于条件概率的积。P(AB/C)=P(A/C)P(B/C)则A、B条件独立(在条件C已知的前提下独立) 或者P(A|C)=P(A|BC)也称为条件独立。
证明：
设A、B、C为事件，P(ABC)＞0，如果P(AB|C)＝P(A|C)P(B|C)，则（ D)
解答：由P(ABC)＞0， P(AB|C)＝P(A|C)P(B|C)
因为若P(A)>0,P(B)>0，P(C)>0不满足，则P(ABC)＞0不成立。
因为P(AB|C)＝P(A|C)P(B|C) ，两边同时乘以P(C) 使左边为P(ABC)
==> P(ABC)=P(AC)*P(B|C)
对（1）式变形，即可得到：P(ABC)/P(AC)=P(B|C)
，只有固定的0和1，即要么发生，要么不发生，从来不会去考虑某件事情发生的概率有多大，不发生的概率又是多大。而且概率
虽然未知，但最起码是一个确定的值。比如如果问那时的人们一个问题：“有一个袋子，里面装着若干个白球和黑球，请问从袋子中取得白球的概率
是多少？”他们会想都不用想，会立马告诉你，取出白球的概率
就是1/2，要么取到白球，要么取不到白球，即θ只能有一个值，而且不论你取了多少次，取得白球的概率θ始终都是1/2，即不随观察结果X
的变化而变化。
这时，
.
,
则
.这种情况称
与
统计独立(statistical
independence)，或 与
独立.
与
不独立也叫
与
统计相依(statistical
dependence).也就是：P(A|B) = P(B) 或者P（A,B) =
P(A)*P(B)多个事件互相独立：
则称
, , 相互独立.条件独立：
条件独立是条件概率的独立性，条件概率也是一种概率，只不过是将事件的空间集合改变。
设有事件R和B,当它们在事件Y定义的空间上相互独立时要满足
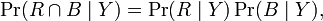
或者表达成
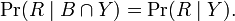
R和B在给定事件W的条件下独立时，表达为
要注意的是，X和Y独立与X和Y条件独立没有关系。显然，条件独立无法推得独立，同样的相互独立也无法保证在任意空间上条件独立。
两个事件关于某一个事件乘积的概率，等于条件概率的积。P(AB/C)=P(A/C)P(B/C)则A、B条件独立(在条件C已知的前提下独立) 或者P(A|C)=P(A|BC)也称为条件独立。
证明：
设A、B、C为事件，P(ABC)＞0，如果P(AB|C)＝P(A|C)P(B|C)，则（ D)
解答：由P(ABC)＞0， P(AB|C)＝P(A|C)P(B|C)
因为若P(A)>0,P(B)>0，P(C)>0不满足，则P(ABC)＞0不成立。
因为P(AB|C)＝P(A|C)P(B|C) ，两边同时乘以P(C) 使左边为P(ABC)
==> P(ABC)=P(AC)*P(B|C)
对（1）式变形，即可得到：P(ABC)/P(AC)=P(B|C)
0 引言
1 贝叶斯方法
，只有固定的0和1，即要么发生，要么不发生，从来不会去考虑某件事情发生的概率有多大，不发生的概率又是多大。而且概率
虽然未知，但最起码是一个确定的值。比如如果问那时的人们一个问题：“有一个袋子，里面装着若干个白球和黑球，请问从袋子中取得白球的概率
是多少？”他们会想都不用想，会立马告诉你，取出白球的概率
就是1/2，要么取到白球，要么取不到白球，即θ只能有一个值，而且不论你取了多少次，取得白球的概率θ始终都是1/2，即不随观察结果X
的变化而变化。1.1 贝叶斯方法的提出
是个不确定的值，因为其中含有机遇的成分。比如，一个朋友创业，你明明知道创业的结果就两种，即要么成功要么失败，但你依然会忍不住去估计他创业成功的几率有多大？你如果对他为人比较了解，而且有方法、思路清晰、有毅力、且能团结周围的人，你会不由自主的估计他创业成功的几率可能在80%以上。这种不同于最开始的“非黑即白、非0即1”的思考方式，便是贝叶斯式的思考方式。- 频率派把需要推断的参数θ看做是固定的未知常数，即概率
- 而贝叶斯派的观点则截然相反，他们认为参数