高斯平面坐标系与迪卡尔坐标系的区别
2013-09-26 13:25阅读：
高斯—克吕格平面直角坐标系简称高斯坐标系（Gauss coordinate
system），是根据高斯—克吕格投影，并以经投影后的中央子午线和赤道这两条相互正交的直线为坐标轴而建立的平面直角坐标系。此坐标系中：中央子午线是纵坐标轴，为x轴，并规定向北（向上）为正方向；赤道是横坐标轴，为Y轴，并规定向东（向右）为正方向；两轴的交点为坐标原点；角度从纵坐标轴（x轴）的正向开始按顺时针方向量取，象限也按顺时针编号。
根据高斯-克吕格尔投影所建立的平面坐标系,或简称高斯平面坐标系。它是大地测量、城市测量、普通测量、各种工程测量和地图制图中广泛采用的一种平面坐标系。高斯-克吕格尔投
影是德国的
C.F.高斯于1822年提出的，后经德国的克吕格尔(J.H.L.Krüger)于1912年加以扩充而完善。用大地经度和纬度表示的大地坐标是一种椭球面上的坐标，不能直接应用于测图。因此，需要将它们按一定的数学规律转换为平面直角坐标。
高斯
平面坐标系表示复数，x轴表示实部，y轴表示虚部，y轴不存在零点。
笛卡尔坐标系用实数组来表示点的位置。
高斯平面直角坐标
- 中文名称：
- 高斯平面坐标系
- 英文名称：
- Gauss plane coordinate system
为了方便工程的规划、设计与施
工，我们需要把测区投影到平面上来，使测量计算和绘图更加方便。而地理坐标是球面坐标，当测区范围较大时，要建平面坐标系就不能乎略地球曲率的影响。把地球上的点位化算到平面上，称为地图投影。地图投影的方法有很多，目前我国采用的是高斯——克吕格投影（又称高斯正形投影），简称高斯投影。它是由德国数学家高斯提出的，由克吕格改进的一种分带投影方法。它成功解决了将椭球面转换为平面的问题。
目录
- 投影方法
- 特点
投影方法
高斯投影的方法是将
地球按经线划分为带，称为投影带。
投影是从首子午线开始的，分6°带和3°两种。每隔6°划分一带的叫6°带，每隔3°划分一带的叫3°带。我国领土位于东经72°∽136°之间，共包括了11个6°带，即13∽23带；22个3°投影带即24∽45带。
设想一个
平面卷成横圆柱套在
地球外，如图1－5（a)所示。通过高斯投影，将中央子午线的投影作为
纵
坐标轴，用x表示，将赤道的投影作横坐标轴，用y表示，两轴的交点作为坐标原点，由此构成的平面直角
坐标系称为高斯
平面直角坐标系，如图1－5（b)
所示。每一个投影带都有一个独立的高斯平面直角坐标系，区分各带坐标系则利用相应投影带的带号。在每一个投影带内，y坐标值都有正有负，这对于计算和使用都不方便，为了使y坐标都为正值，故将纵坐标轴向西
平移500㎞，并在y坐标前加上投影带的带号。 6°带投影是从
英国格林尼治子午线开始，自西向东，每隔经差6°分为一带，将地球分为60个带，其编号分别为1，2，3，…60。任意带的
中央子午线经度为Lo，它与投影带号N的关系如下所示：
Lo=(6N-3°)
式中：N———6°带的带号
离中央子午线越远，长度变形越大，在要求较小的投影变形时，可采用3°投影带。3°带是在6°带的基础上划分的，如图所示。每3°为一带，从东经1°30′开始，共120带，其中央子午线在奇数带时与6°带的中央子午线重合，每带的中央子午线可用下面的工式计算：
Lo=3N′
式中：N′——3°带的带号。
为了避免y坐标出现
负值，3°带的坐标原点同6°带一样，向西移动500㎞，并在y坐标前加3°带的带号。
特点
应当注意的是，高斯投影没的角度变形，但有长度变形和面积变形，离中央子午线越远，变形就越大。其主要特点有以下三点：
（1）投影后中央子午线为直线，长度不变形，其余经线投影对称并且凹向于中央子午线，离中央子午线越远，变形越大。
（2）赤道的投影也为一直线，并与中央子午线正交，其余的经纬投影为凸向赤道的对称曲线。
（3）经纬投影后仍然保持相互垂直的关系，投影后有角度无变形。
此坐标系中：中央子午线是纵坐标轴，为x轴，并规定向北（向上）为正方向；赤道是横坐标轴，为Y轴，并规定向东（向右）为正方向；两轴的交点为坐标原点；角度从纵坐标轴（x轴）的正向开始按顺时针方向量取，象限也按顺时针编号
http://wenku.baidu.com/view/6736c03467ec102de2bd8969.html
http://www.doc88.com/p-582425552229.html
大地坐标系是大地测量的基本坐标系。常用于大地问题的细算，研究地球形状和大小，编制地图，火箭和卫星发射及军事方面的定位及运算，若将其直接用于工程建设规划、设计、施工等很不方便。所以要将球面上的大地坐标按一定数学法则归算到平面上，即采用地图投影的理论绘制地形图，才能用于规划建设。
椭球体面是一个不可直接展开的曲面，故将椭球体面上的元素按一定条件投影到平面上，总会产生变形。测量上常以投影变形不影响工程要求为条件选择投影方法。地图投影有等角投影、等面积投影和任意投影三种。
其中等角投影又称为正形投影，它保证在椭球体面上的微分图形投影到平面后将保持相似。这是地形图的基本要求。正形投影有两个基本条件：
①保角条件，即投影后角度大小不变。
②长度变形固定性，即长度投影后会变形，但是在一点上各个方向的微分线段变形比m是个常数k：
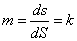
式中：ds—投影后的长度，dS—球面上的长度。
1.高斯投影的概念
高斯是德国杰出的数学家、测量学家。他提出的横椭圆柱投影是一种正形投影。它是将一个横椭圆柱套在地球椭球体上，如下图所示：
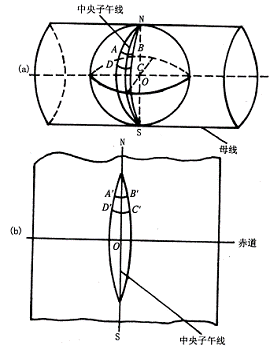
椭球体中心O在椭圆柱中心轴上，椭球体南北极与椭圆柱相切，并使某一子午线与椭圆柱相切。此子午线称中央子午线。然后将椭球体面上的点、线按正形投影条件投影到椭圆柱上，再沿椭圆柱N、S点母线割开，并展成平面，即成为高斯投影平面。在此平面上：
①中央子午线是直线，其长度不变形，离开中央子午线的其他子午线是弧形，凹向中央子午线。离开中央子午线越远，变形越大。
②投影后赤道是一条直线，赤道与中央子午线保持正交。
③离开赤道的纬线是弧线，凸向赤道。
高斯投影可以将椭球面变成平面，但是离开中央子午线越远变形越大，这种变形将会影响测图和施工精度。为了对长度变形加以控制，测量中采用了限制投影宽度的方法，即将投影区域限制在靠近中央子午线的两侧狭长地带。这种方法称为分带投影。投影带宽度是以相邻两个子午线的经差来划分。有6°带、3°带等不同投影方法。
6°带投影是从英国格林尼治子午线开始，自西向东，每隔6°投影一次。这样将椭球分成60个带，编号为1～60带，如下图所示：
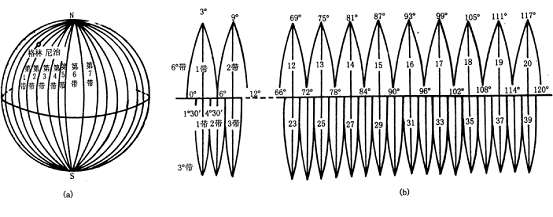
各带中央子午线经度(L)可用下式计算：
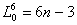
式中n为6°带的带号。
已知某点大地经度L，可按下式计算该点所属的带号：
有余数时，为n的整数商+1。
3°带是在6°带基础上划分的，其中央子午线在奇数带时与6°带中央子午线重合，每隔3°为一带，共120带，各带中央子午线经度(L)为：
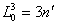
式中n′为3°带的带号。
我国幅员辽阔，含有11个6°带，即从13～23带(中央子午线从75°～135°)，21个3°带，从25～45带。北京位于6°带的第20带，中央子午线经度为117°。
2.高斯平面直角坐标系
根据高斯投影的特点，以赤道和中央子午线的交点为坐标原点。，中央子午线方向为x轴，北方向为正。赤道投影线为y轴，东方向为正。象限按顺时针Ⅰ、Ⅱ、Ⅲ、Ⅳ排列，如下图所示：
在同一投影带内y值有正有负。这对计算和使用很不方便。为了使y值都为正，将纵坐标轴西移500km，并在y坐标前面冠以带号，如在第20带，中央子午线以西P点：
在20带中高斯直角坐标为：
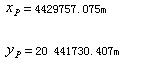
高斯直角坐标系与数学中的笛卡尔坐标系不同，如下图所示：
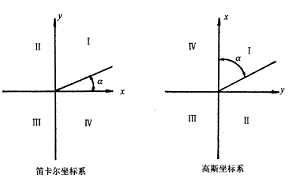
高斯直角坐标系纵坐标为x轴，横坐标为y轴。坐标象限为顺时针划分四个象限。角度起算是从x轴的北方向开始，顺时针计算。这些定义都与数学中的定义不同。这样的做法是为了将数学上的三角和解析几何公式直接用到测量的计算上。
