系统进化树介绍
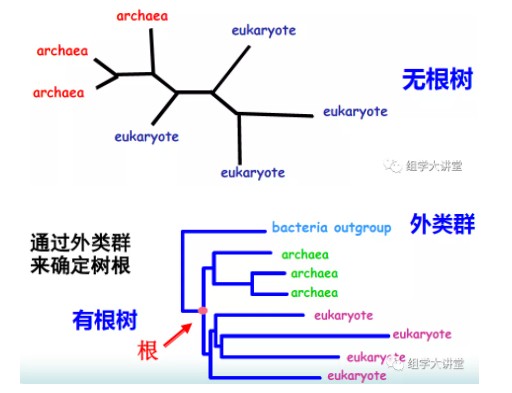
研究分子进化所要构建的系统发生树(Phylogenetic tree),也叫分子树,对于一个未知的基因或蛋白质序列,可以利用系统发生树确定与其亲缘关系最近的物种。比如你得到了一个新发现的细菌的核糖体RNA,你可以将它跟所有已知的核糖体RNA放在一起,然后用他们构建一棵系统发生树。这样就可以从树上推测出谁和这个新细菌的关系最近。系统发生树还可以预测一个新发现的基因或蛋白质的功能。系统发生树还分为有根树和无根树(下图),顾名思义,有根树就是有根,无根树就是无根。其实两者是可以互换的。如果我们按住无根树上某一个点,然后用把梳子将树上所有的枝条都以这个点为中心向右梳理,就能把它梳成有根树的样子。按住的这个点就是根。所以对于一棵树来说,根的位置是主观的,你想让他在哪它就在哪里。但是你不能随意指定哪个内节点当根,毕竟根有其自身的生物学意义,它应该是所有叶子的共同祖先。那么我们如何确定根的位置呢?可以通过外类群(outgroup)来确定,从而把无根树变成有根树。有根树反映了树上基因或蛋白质进化的时间顺序,通过分析有根树的树枝的长度,可以了解不同的基因或蛋白质以什么方式和速率进化。而无根树只反映分类单元之间的距离,而不涉及谁是谁的祖先问题。做有根树需要指定外类群。所谓外类群,就是你所研究的内容之外的一个群。比如你要分析某一个基因在不同人种间的进化关系,那就可以额外选择黑猩猩加入进来,作为外类群一同参与建树。