普朗克电子谐振子与玻尔电子轨道跃迁的内在联系
司今(jiewaimuyu@126.com)
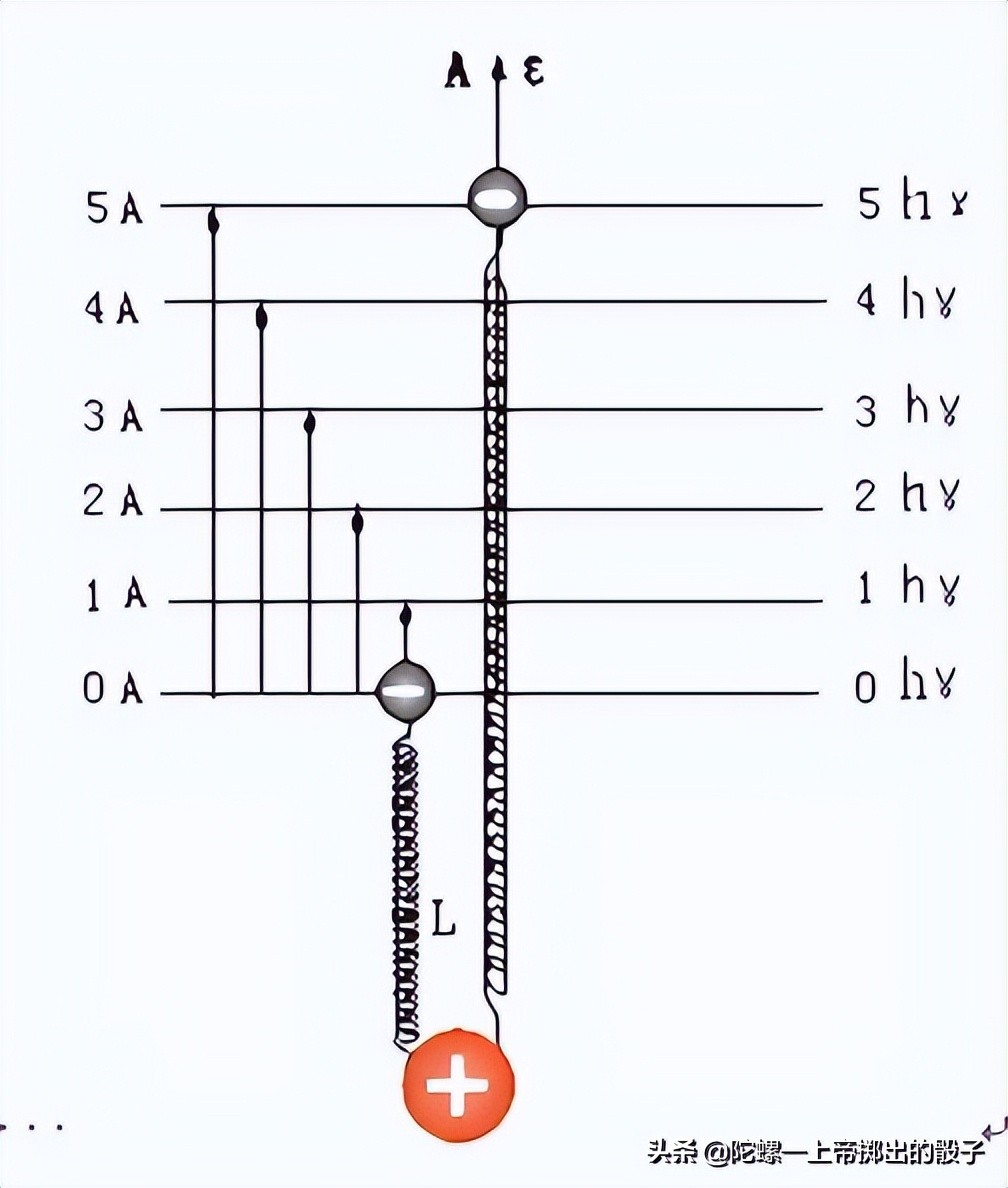
图-1.普朗克一维电子谐振子
普朗克在解决黑体辐射难题时认为,黑体辐射能量是由一维电子谐振子振动所产生的,如图-1所示,且电子谐振子振动发射或吸收的能量是不连续的,即量子化的;后来,爱因斯坦在解释光电效应时,将这种量子化能量延伸为光量子概念,即今天所说的光子;再后来,玻尔为解决卢瑟福原子稳定性难题,提出了电子轨道能级理论,并假设电子轨道跃迁时会释放光子。
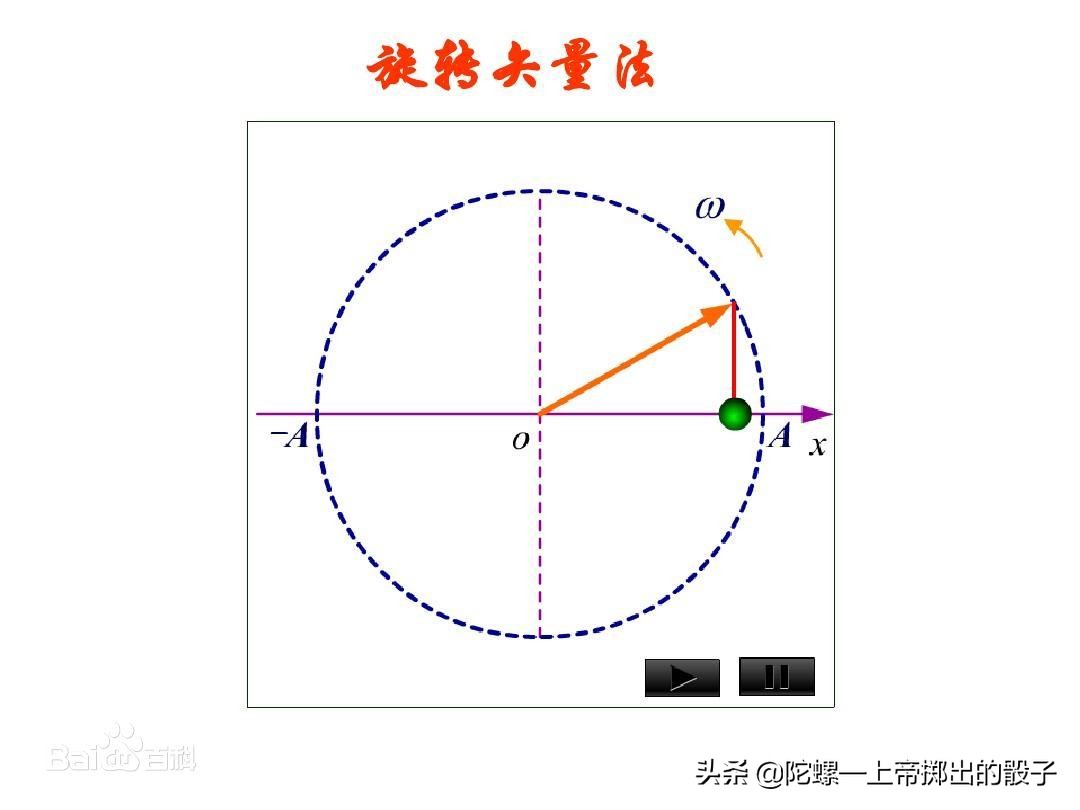 图-2.旋转矢量
图-2.旋转矢量
从经典物理学角度来看,一维谐振子振动可以用几何化的旋转矢量法进行较为直观的描述,即如图-2所示,从坐标原点O(平衡位置)画一矢量 ,使它的模等于谐振动的振幅A,并
司今(jiewaimuyu@126.com)
图-1.普朗克一维电子谐振子
普朗克在解决黑体辐射难题时认为,黑体辐射能量是由一维电子谐振子振动所产生的,如图-1所示,且电子谐振子振动发射或吸收的能量是不连续的,即量子化的;后来,爱因斯坦在解释光电效应时,将这种量子化能量延伸为光量子概念,即今天所说的光子;再后来,玻尔为解决卢瑟福原子稳定性难题,提出了电子轨道能级理论,并假设电子轨道跃迁时会释放光子。
从经典物理学角度来看,一维谐振子振动可以用几何化的旋转矢量法进行较为直观的描述,即如图-2所示,从坐标原点O(平衡位置)画一矢量 ,使它的模等于谐振动的振幅A,并
