新浪博客
说明 示例
示例
定义域。
z = 0:0.1:20;
计算前五个第一类贝塞尔函数。
J = zeros(5,201); for i = 0:4 J(i+1,:) = besselj(i,z); end
在同一图窗中绘制所有函数。
plot(z,J) grid on legend('J_0','J_1','J_2','J_3','J_4','Location','Best') title('Bessel Functions of the First Kind for $u \in [0, 4]$','interpreter','latex') xlabel('z','interpreter','latex') ylabel('$J_u(z)$','interpreter','latex')
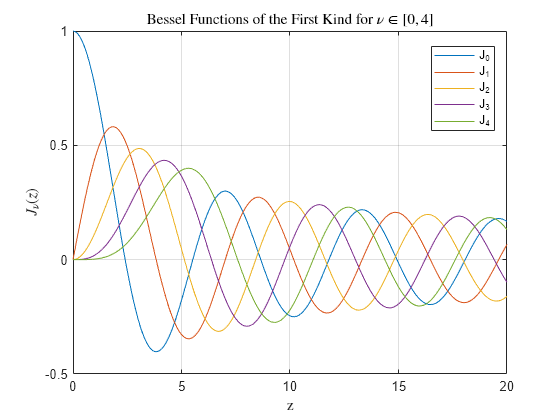
为
x = -10:0.3:10; y = x'; z = x + 1i*y; scale = 1; J = besselj(2,z); Js = besselj(2,z,scale);
比较经过缩放的函数和未缩放函数的虚部图。对于
surf(x,y,imag(J)) title('Bessel Function of the First Kind','interpreter','latex') xlabel('real(z)','interpreter','latex') ylabel('imag(z)','interpreter','latex')
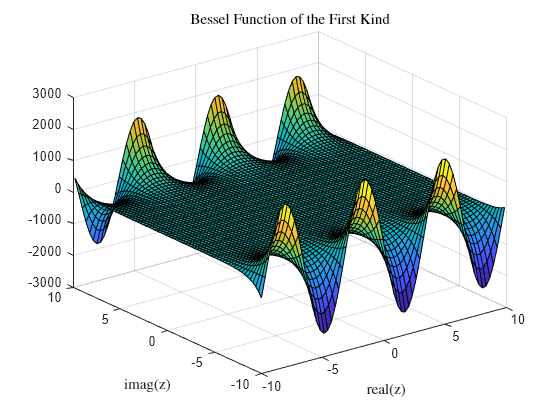
surf(x,y,imag(Js)) title('Scaled Bessel Function of the First Kind','interpreter','latex') xlabel('real(z)','interpreter','latex') ylabel('imag(z)','interpreter','latex')
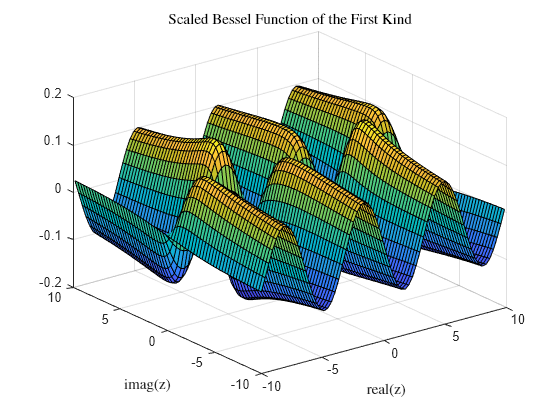
方程的阶,指定为标量、向量、矩阵或多维数组。
示例:
数据类型:
函数的域,指定为标量、向量、矩阵或多维数组。
示例:
J = besselj(nu,Z) Z 示例
J = besselj(nu,Z,scale)
scale 1,则
besselj exp(-abs(imag(Z))) 示例
全部折叠绘制第一类贝塞尔函数图
定义域。
z = 0:0.1:20;
计算前五个第一类贝塞尔函数。
J z J = zeros(5,201); for i = 0:4 J(i+1,:) = besselj(i,z); end
在同一图窗中绘制所有函数。
plot(z,J) grid on legend('J_0','J_1','J_2','J_3','J_4','Location','Best') title('Bessel Functions of the First Kind for $u \in [0, 4]$','interpreter','latex') xlabel('z','interpreter','latex') ylabel('$J_u(z)$','interpreter','latex')

计算呈指数缩放的贝塞尔函数
为
J) 和经过缩放的
(Js) 第一类贝塞尔函数
x = -10:0.3:10; y = x'; z = x + 1i*y; scale = 1; J = besselj(2,z); Js = besselj(2,z,scale);
比较经过缩放的函数和未缩放函数的虚部图。对于
abs(imag(z))
surf(x,y,imag(J)) title('Bessel Function of the First Kind','interpreter','latex') xlabel('real(z)','interpreter','latex') ylabel('imag(z)','interpreter','latex')

surf(x,y,imag(Js)) title('Scaled Bessel Function of the First Kind','interpreter','latex') xlabel('real(z)','interpreter','latex') ylabel('imag(z)','interpreter','latex')

输入参数
全部折叠
nu
标量
方程的阶,指定为标量、向量、矩阵或多维数组。
nu
nu Z
示例:
besselj(3,0:5)数据类型:
single double
Z
标量
函数的域,指定为标量、向量、矩阵或多维数组。
besselj
Z
nu Z 示例:
