X²+1素数
2014-07-15 05:07阅读:
X²+1素数问题是与哥德巴赫猜想和孪生素数猜想同时代的著名数学难题。是否有无穷个正整数x,使得x²+1总是素数?
其困难程度不亚于哥德巴赫猜想。特别是100多年以来,许许多多一流数论学者对这个问题进行了研究。
X²+1素数
X²+1素数是一个著名的猜想,人们很早就发现了许多正整数的平方加1以后是素数,例如:
1²+1=2,素数;2²+1=5,素数;4²+1=17,素数;
6²+1=37,素数;10²+1=101,素数;14²+1=197,素数;
16²+1=257,素数; 20²+1=401,是素数;24²+1=577,是素数;
....。
这种类型素数有多少?是否有无穷个?这就是X²+1素数猜想。这个问题其实已经有几百年了,仍然没有得到解决。
这个问题为什么著名
1900年,在法国巴黎召开了第二届国际数学家大会,全能的数学大师希尔伯特发表了{未来的数学问题}这个著名的讲演,
在第25自然段谈到这个问题,问是否有无穷个x²+1素数(参见希尔伯特23个问题),而且还与费马数有关(参见下面其它相关书籍)
这个问题为什么这么困难
与哥德巴赫猜想和孪生素数猜想一样,这个问题的解决依靠普遍的
素数公式的解决。没有一个可以表示所有素数的普遍公式,
问题是不能获得解决(参见
素数判定法则 )。
X²+1素数的公式
“若自然数n不能被不大于

任何素数 整除,则n是一个素数”。 代数学辞典 上海教育出版社 1985年
259页。参见
素数。
如果设n=X²+1。则可以用公式表达:

.(1)
其中
 表示顺序素数2,3,5,....。
表示顺序素数2,3,5,....。 
≠

。 即X≠

形。
若

,则X²+1是一个素数。
我们可以把(1)式内容等价转换成为同余式组表示:

由于(2)的模

,

,...,
 两两互素,根据孙子定理(中国剩余定理)知,对于给定的
两两互素,根据孙子定理(中国剩余定理)知,对于给定的  值,(2)式在
值,(2)式在 

...

范围内有唯一解。
例题
k=1时,

,解得X=2。2<3=

.得知2²+1=5是素数。 求得了(3,3²)区间的全部X²+1型素数。
k=2时,

,解得X=4;4<5=

;4²+1=17是素数.

,解得X=8;8≮5=

,所以8不是我们要的数;

,解得X=6;6≮5=

,所以6不是我们要的数;
求得了(5,5²)区间的全部素数X²+1型素数(仅有一个17)。
k=3时,

。解得X=6,6<7=

。6²+1=37,是素数。
求得了(7,7²)区间的全部X²+1型素数。 k=4时,

。解得X=10,10<11=
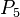
。10²+1是素数。
求得了(11,11²)区间的全部素数。
仿此下去可以求得任意大的数以内的全部X²+1素数。并且一个不漏地求得。
为什么我们不能用

和

?对于模为5时,

。 因为

≠

。即±2=

。
因为,如果X=5m±2,X²+1=(5m±2)²+1=25m²±10m+5=5(5m²±2m+1)是一个复合数。
同样,我们不能用

;

;...。
因为有定理(参见《基础数论》92页,U杜德利著,上海教育出版社):假定P为奇素数,若P不能够整除a,
则X²≡a(modP),恰有两解或者无解。
有理域知识
有理域通常称为伽罗华域,只有素数和它们的幂才有有限域。
A²=A×A.(例如A有5个元素的域;0,1,2,3,4),因为减2总是可以用加3代替,反之亦然。
对于除法也是一样,因为2的乘法逆元素是3,即2×3=1,所以除以2的除法总是可以用乘以3的乘法表示。
其它书籍相关内容
《数论导引》18页(人民邮电出版社):是否存在无穷多个x²+1素数,更一般地,如果a,b,c是没有公约数的整数,a是正数,a+b和c不全是偶数,并且b²-4ac不是完全平方数,那么,就有无穷多个形如:ax²+bx+c的素数存在。
《10000个科学难题》数学卷102页,(科学出版社2009年5月第一版):是否有无穷个正整数x,使得x²+1总是素数?这个问题比孪生素数猜想更加困难,这是因为在正整数中,形如x²+1的数必p+2稀少,所以x²+1为素数的概率更小。
《数论中未解决问题》75页(【加】R.K盖伊著,张明尧译)形如x²+1素数是很少的,但是,如果只有有限个,那么,就可以推出有无限多个费马数是复合数。
X²+1合数与佩尔方程
由于问题的困难,人们开始关注X²+1合数,企图从X²+1合数的蛛丝马迹中寻找X²+1素数。发现许许多多X²+1合数有平方因子
例如:18²+1=325=5²×13;32²+1=2025=5²×41;38²+1=1445=5×17²;68²+1=4625=5³×37;70²+1=4901=13²×29;....。
这是一个佩尔方程形式:

38²-5×17²=-1;68²-29×13²=-1。
参见

 任何素数 整除,则n是一个素数”。 代数学辞典 上海教育出版社 1985年
259页。参见
任何素数 整除,则n是一个素数”。 代数学辞典 上海教育出版社 1985年
259页。参见 .(1)
.(1) 表示顺序素数2,3,5,....。
表示顺序素数2,3,5,....。  ≠
≠  。 即X≠
。 即X≠  形。
形。 ,则X²+1是一个素数。
,则X²+1是一个素数。
 ,
,  ,...,
,..., 
 值,(2)式在
值,(2)式在  ,解得X=2。2<3=
,解得X=2。2<3=  .得知2²+1=5是素数。 求得了(3,3²)区间的全部X²+1型素数。
.得知2²+1=5是素数。 求得了(3,3²)区间的全部X²+1型素数。 ,解得X=4;4<5=
,解得X=4;4<5=  ;4²+1=17是素数.
;4²+1=17是素数. ,解得X=8;8≮5=
,解得X=8;8≮5=  ,解得X=6;6≮5=
,解得X=6;6≮5=  。解得X=6,6<7=
。解得X=6,6<7=  。6²+1=37,是素数。
。6²+1=37,是素数。 。解得X=10,10<11=
。解得X=10,10<11= 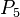 。10²+1是素数。
。10²+1是素数。 和
和  ?对于模为5时,
?对于模为5时,  。 因为
。 因为  。
因为,如果X=5m±2,X²+1=(5m±2)²+1=25m²±10m+5=5(5m²±2m+1)是一个复合数。
。
因为,如果X=5m±2,X²+1=(5m±2)²+1=25m²±10m+5=5(5m²±2m+1)是一个复合数。 ;
;  ;...。
;...。