1:信息视角下的无序与有序:
当代的复杂性科学提供了一套揭示世界的原理和语言,如耗散结构理论,自组织理论,分形数学,泛系统论,协同论,突变论,信息论等等,具体应用起来,却殊为不易。不过,以它的基本原理为基础,也不是无可作为。
任何一种有序状态的出现都可以看作是某种无序的参考态失去稳定性的结果。这是耗散结构理论的一个结论。
从信息的角度看,这句话似乎可以这样来理解:有序状态对应的是信息丰富的状态,无序状态对应的是信息贫乏的状态。比如统计学中的均匀分布或随机游走分布模型就代表了信息贫乏的状态即无序状态,而如果一个系统不属于均匀分布或随机游走,即均匀分布或随机游走的否定,就等于肯定了该系统具有信息,或者说具有某种程度的有序性。
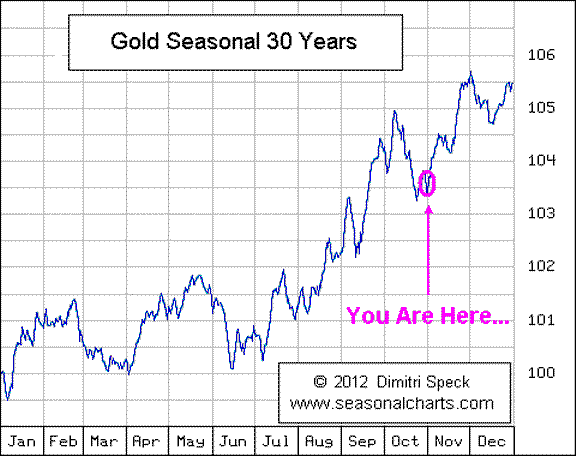
设有某种均匀分布的宏观状态,比如股市,它就有“随机漫步”一说或者说是均匀分布的平衡态。我们可以用图表示如下:X轴可以是某项主要的物理量,如股市中的成交额,Y轴代表空间,如股市的价格指数;红色虚直线可以代表某种均匀分布的宏观状态,蓝色实线代表系统的实际状态,由于存在涨落现象而导致实际状态并非如虚线所示。涨落的大小可能很小,但空间行为是完全任意的,杂乱无章的,正如蓝色实线所示的那样。不过总可以把该蓝色实线看作是红色虚直线与大量的涨落的傅立叶分量叠加而成的。

当代的复杂性科学提供了一套揭示世界的原理和语言,如耗散结构理论,自组织理论,分形数学,泛系统论,协同论,突变论,信息论等等,具体应用起来,却殊为不易。不过,以它的基本原理为基础,也不是无可作为。
任何一种有序状态的出现都可以看作是某种无序的参考态失去稳定性的结果。这是耗散结构理论的一个结论。
从信息的角度看,这句话似乎可以这样来理解:有序状态对应的是信息丰富的状态,无序状态对应的是信息贫乏的状态。比如统计学中的均匀分布或随机游走分布模型就代表了信息贫乏的状态即无序状态,而如果一个系统不属于均匀分布或随机游走,即均匀分布或随机游走的否定,就等于肯定了该系统具有信息,或者说具有某种程度的有序性。
设有某种均匀分布的宏观状态,比如股市,它就有“随机漫步”一说或者说是均匀分布的平衡态。我们可以用图表示如下:X轴可以是某项主要的物理量,如股市中的成交额,Y轴代表空间,如股市的价格指数;红色虚直线可以代表某种均匀分布的宏观状态,蓝色实线代表系统的实际状态,由于存在涨落现象而导致实际状态并非如虚线所示。涨落的大小可能很小,但空间行为是完全任意的,杂乱无章的,正如蓝色实线所示的那样。不过总可以把该蓝色实线看作是红色虚直线与大量的涨落的傅立叶分量叠加而成的。