债券-久期与凸性(概念与应用)
2017-07-11 11:18阅读:
久期和凸性是衡量债券利率风险的重要指标。
久期也称持续期,是以未来时间发生的现金流,按照目前的收益率折现成现值,再用每笔现值乘以其距离债券到期日的年限求和,然后以这个总和除以债券目前的价格得到的数值。
久期描述了价格-收益率曲线的斜率,凸性描述了价格/收益率曲线的弯曲程度。凸性是债券价格对收益率的二阶导数。
别看概念!看应用!
如果一只债券收益率下降了10BP,大概涨了多少钱?
10BP * 久期
例如一只4.5久期的债券收益率下降10BP大概上涨了4.5 * 10=45
也就是0.45元
例如一只2久期的债券收益率上涨10BP大概下跌了2 * 10=20也就是0.2元
如果债券市场上涨,什么样的券涨得更多?
久期长,凸性大
通俗点的说法:
久期:与期限相关,可以反映价格对利率变动的敏感性,久期越长,对利率敏感性越高。
凸性:债券涨跌的弹性。
---------------------------------------------------------------------------------------------------------
概念篇:
久期
久期(也称持续期)是1938年由F.R.Macaulay提出的,用来衡量债券的到期时间。它是以未来收益的现值为权数计算的到期时间。久期收益率变化1%所引起的债券全价变化的百分比。久期用来衡量债券价格对利率变化的敏感性。
债券的久期越大,利率的变化对该债券价格的影响也越大,因此风险也越大。在降息时,久期大的债券上升幅度较大;在升息时,久期大的债券下跌的幅度也较大。因此,投资者在预期未来降息时,可选择久期大的债券;在预期未来升息时,可选择久期小的债券。
 修正久期
修正久期是用来衡量债券价格对利率变化的敏感程度的指标。
具体地说,有公式
修正久期
修正久期是用来衡量债券价格对利率变化的敏感程度的指标。
具体地说,有公式
 其中,dy表示收益率的变化,dP表示价格的变化,D*表示修正久期,C表示凸性。
修正久期的具体计算公式为
其中,dy表示收益率的变化,dP表示价格的变化,D*表示修正久期,C表示凸性。
修正久期的具体计算公式为
 修正久期度量了收益率与债券价格的近似线性关系,即到期收益率变化时债券价格的稳定性。在同等要素条件下,修正久期小的债券较修正久期大的债券抗利率上升风险能力强,但抗利率下降风险能力较弱。
凸性
利用久期衡量债券的利率风险具有一定的误差,债券价格随利率变化的波动性越大,这种误差越大。凸性可以衡量这种误差。
凸性是对债券价格曲线弯曲程度的一种度量。凸性越大,债券价格曲线弯曲程度越大,用修正久期度量债券的利率风险所产生的误差越大。严格地定义,凸性是指在某一到期收益率下,到期收益率发生变动而引起的价格变动幅度的变动程度。
凸性的具体计算公式为
修正久期度量了收益率与债券价格的近似线性关系,即到期收益率变化时债券价格的稳定性。在同等要素条件下,修正久期小的债券较修正久期大的债券抗利率上升风险能力强,但抗利率下降风险能力较弱。
凸性
利用久期衡量债券的利率风险具有一定的误差,债券价格随利率变化的波动性越大,这种误差越大。凸性可以衡量这种误差。
凸性是对债券价格曲线弯曲程度的一种度量。凸性越大,债券价格曲线弯曲程度越大,用修正久期度量债券的利率风险所产生的误差越大。严格地定义,凸性是指在某一到期收益率下,到期收益率发生变动而引起的价格变动幅度的变动程度。
凸性的具体计算公式为
 当两个债券的久期相同时,它们的风险不一定相同,因为它们的凸性可能是不同的。
当两个债券的久期相同时,它们的风险不一定相同,因为它们的凸性可能是不同的。
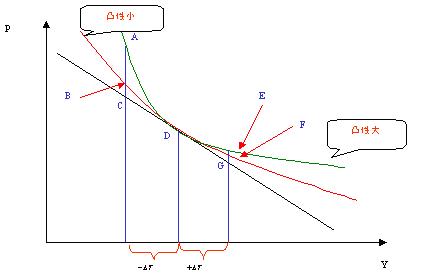 如图所示,两个债券的收益率与价格的关系为红线与绿线,内侧的曲线(绿线)为凸性大的曲线,外侧的曲线为凸性小的曲线(红线)。在收益率增加相同单位时,凸性大的债券价格减少幅度较小;在收益率减少相同单位时,凸性大的债券价格增加幅度较大。因此,在久期相同的情况下,凸性大的债券其风险较小。
由于修正久期度量的是债券价格和到期收益率的近似线性关系,由此计算得出的债券价格变动幅度存在误差,而凸性值对这种误差进行了调整。
如图所示,两个债券的收益率与价格的关系为红线与绿线,内侧的曲线(绿线)为凸性大的曲线,外侧的曲线为凸性小的曲线(红线)。在收益率增加相同单位时,凸性大的债券价格减少幅度较小;在收益率减少相同单位时,凸性大的债券价格增加幅度较大。因此,在久期相同的情况下,凸性大的债券其风险较小。
由于修正久期度量的是债券价格和到期收益率的近似线性关系,由此计算得出的债券价格变动幅度存在误差,而凸性值对这种误差进行了调整。
----------------------------------------------------------------------------------------------------------
应用篇:
久期是以未来时间发生的现金流,按照目前的收益率折现成现值,再用每笔现值乘以其距离债券到期日的年限求和,然后以这个总和除以债券目前的价格得到的数值..
数学定义 :如果市场利率是Y,现金流(X1,X2,...,Xn)的麦考雷久期定义为:
D(Y)=[1*X1/(1+Y)^1+2*X2/(1+Y)^2+...+n*Xn/(1+Y)^n]/[X0+x1/(1+Y)^1+X2/(1+Y)^2+...+Xn/(1+Y)^n]
即 D=(1*PVx1+...n*PVxn)/PVx 其中,PVXi表示第i期现金流的现值,D表示久期。
例子:假设有一债券,在未来n年的现金流为(X1,X2,...Xn),其中Xi表示第i期的现金流。假设现在利率为Y0,投资者持有现金流不久,利率立即发生变化,变为Y,问:应该持有多长时间,才能使得其到期的价值不低于现在的价值?
通过下面定理可以快速解答上面问题。
定理:PV(Y0)*(1+Y0)^q<=PV(Y)(1+Y)^q的必要条件是q=D(Y0)。这里D(Y0)=
(X1/(1+Y0)+2*X2/(1+Y0)^2+...+n*Xn/(1+Y0)^n)/PV(Y0)
q即为所求时间,即为久期。
上述定理的证明可通过对Y导数求倒数,使其在Y=Y0取局部最小值得到。(容易)
----------------------------------------------------------------------------------------------------------
经验总结:
在债券分析中,久期已经超越了时间的概念,投资者更多地把它用来衡量债券价格变动对利率变化的敏感度,并且经过一定的修正,以使其能精确地量化利率变动给债券价格造成的影响。修正久期越大,债券价格对收益率的变动就越敏感,收益率上升所引起的债券价格下降幅度就越大,而收益率下降所引起的债券价格上升幅度也越大。可见,同等要素条件下,修正久期小的债券比修正久期大的债券抗利率上升风险能力强,但抗利率下降风险能力较弱。
正是久期的上述特征给我们的债券投资提供了参照。当我们判断当前的利率水平存在上升可能,就可以集中投资于短期品种、缩短债券久期;而当我们判断当前的利率水平有可能下降,则拉长债券久期、加大长期债券的投资,这就可以帮助我们在债市的上涨中获得更高的溢价.
需要说明的是,久期的概念不仅广泛应用在个券上,而且广泛应用在债券的投资组合中。一个长久期的债券和一个短久期的债券可以组合一个中等久期的债券投资组合,而增加某一类债券的投资比例又可以使该组合的久期向该类债券的久期倾斜。所以,当投资者在进行大资金运作时,准确判断好未来的利率走势后,然后就是确定债券投资组合的久期,在该久期确定的情况下,灵活调整各类债券的权重,基本上就能达到预期的效果。
久期是一种测度债券发生现金流的平均期限的方法。由于债券价格敏感性会随着到期时间的增长而增加,久期也可用来测度债券对利率变化的敏感性,根据债券的每次息票利息或本金支付时间的加权平均来计算久期。
久期的计算就当是在算加权平均数。其中变量是时间,权数是每一期的现金流量,价格就相当于是权数的总和(因为价格是用现金流贴现算出来的)。这样一来,久期的计算公式就是一个加权平均数的公式了,因此,它可以被看成是收回成本的平均时间。
决定久期即影响债券价格对市场利率变化的敏感性包括三要素:到期时间、息票利率和到期收益率。
不同债券价格对市场利率变动的敏感性不一样。债券久期是衡量这种敏感性最重要和最主要的标准。久期等于利率变动一个单位所引起的价格变动。如市场利率变动1%,债券的价格变动3%,则久期是3。
马考勒久期定理
定理一:只有贴现债券的马考勒久期等于它们的到期时间。
定理二:直接债券的马考勒久期小于或等于它们的到期时间。
定理三:统一公债的马考勒久期等于(1+1/y),其中y是计算现值采用的贴现率。
定理四:在到期时间相同的条件下,息票率越高,久期越短。
定理五:在息票率不变的条件下,到期时间越久,久期一般也越长。
定理六:在其他条件不变的情况下,债券的到期收益率越低,久期越长。
实际上,久期在数值上和债券的剩余期限近似,但又有别于债券的剩余期限。在债券投资里,久期被用来衡量债券或者债券组合的利率风险,它对投资者有效把握投资节奏有很大的帮助。一般来说,久期和债券的到期收益率成反
比,和债券的剩余年限成正比,和票面利率成反比。一个特殊的情况是,当一个债券是贴现发行的无票面利率债券,那么该债券的剩余年限就是其久期。这也是为什么人们常常把久期和债券的剩余年限相提并论的原因。
利用久期进行免疫
所谓免疫,就是构建这样的一个投资组合,在组合内部,利率变化对债券价格的影响可以互相抵消,因此组合在整体上对利率不具有敏感性。而构建这样组合的基本方法就是通过久期的匹配,使附息债券可以精确地近似于一只零息债券。利用久期进行免疫是一种消极的投资策略,组合管理者并不是通过利率预测去追求超额报酬,而只是通过组合的构建,在回避利率波动风险的条件下实现既定的收益率目标。在组合品种的设计中,除了国债可以选入组合外,部分收益率较高的企业债券及金融债券也能加入投资组合,条件是控制好匹配的久期。
但是,免疫策略本身带有一定的假设条件,比如收益率曲线的变动不是很大,到期收益率的高低与市场利率的变化之间有一个平衡点,一旦收益率确实发生了很大的变动,则投资组合不再具有免疫作用,需要进行再免疫,或是再平衡;其次,免疫严格限定了到期支付日,对于那些支付或终止期不能确定的投资项目而言并不是最优;再次,投资组合的免疫作用仅对于即期利率的平行移动有效,对于其他变动,需要进一步拓展应用。
利用久期优化投资组合
进行免疫后的投资组合,虽然降低了利率波动的风险,但是组合的收益率却会偏低。为了实现在免疫的同时也能增加投资的收益率,可以使用回购放大的办法,来改变某一个债券的久期,然后修改免疫方程式,找到新的免疫组合比例,这样就可以提高组合的收益率。但是,在回购放大操作的同时,投资风险也在同步放大,因此要严格控制放大操作的比例。
具体实践与分析
各个时段的敏感性权重通常是由假定的利率变动乘以该时段头寸的假定平均久期来确定。一般而言,金融工具的到期日或距下一次重新定价日的时间越长,并且在到期日之前支付的金额越小,则久期的绝对值越高,表明利率变动将会对银行的经济价值产生较大的影响。久期分析也是对利率变动进行敏感性分析
的方法之一。
银行可以对以上的标准久期分析法进行演变,如可以不采用对每一时段头寸使用平均久期的做法,而是通过计算每项资产、负债和表外头寸的精确久期来计量市场利率变化所产生的影响,从而消除加总头寸/现金流量时可能产生的误差。另外,银行还可以采用有效久期分析法,即对不同的时段运用不同的权重,根据在特定的利率变化情况下,假想金融工具市场价值的实际百分比变化,来设计各时段风险权重,从而更好地反映市场利率的显著变动所导致的价格的非线性变化。
与缺口分析相比较,久期分析是一种更为先进的利率风险计量方法。缺口分析侧重于计量利率变动对银行短期收益的影响,而久期分析则能计量利率风险对银行经济价值的影响,即估算利率变动对所有头寸的未来现金流现值的潜在影响,从而能够对利率变动的长期影响进行评估,更为准确地估算利率风险对银行的影响。但是,久期分析仍然存在一定的局限性。第一,如果在计算敏感性权重时对每一时段使用平均久期,即采用标准久期分析法,久期分析仍然只能反映重新定价风险,不能反映基准风险,以及因利率和支付时间的不同而导致的头寸的实际利率敏感性差异,也不能很好地反映期权性风险。第二,对于利率的大幅变动(大于1%),由于头寸价格的变化与利率的变动无法近似为线性关系,因此,久期分析的结果就不再准确。




